Question 41123: How do you find the vertex when you have a word problem?
The word problem: A company sells 80 team jackets a week for $30 each. The product manager estimates that for each $3 increase in price, the company will sell 5 fewer jackets per week. What price should be charged per jacket to maximize the profit?
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! If they're looking to maximize profit, the curve should
have a peak instead of a dip.
Let x = the number of $3 increases in price.
According to the problem, 5x fewer jackets per week will be
sold with x number of $3 increases in price
The price per jacket is
The corresponding number of jackets sold is
Let income from sales of jackets = I
I assume if income is maximized, profit will also be maximized
factor out 3 from (30 - 3x) and 5 from (80 - 5x)
The  signals that the curve has a positive peak
use
 , 
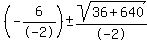
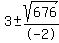
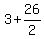3 + 13 and 3 - 13 are the answers, or
16 and -10
This is where the meaaning of vertex comes in. 16 and -10
are the solutions to  which gives
us the ROOTS of the equation, the values of x that make it zero,
or in this case, NO income.
So, we don't want the roots, what do we want?
We want the value of x midway between the roots
3 is midway between -10 and 16.
-10 is at 3 -13
16 is at 3 + 13
What price should be charged per jacket to maximize the profit?
That's what the problem wants
 is the price per jacket
$39 per jacket is the answer
Check the answer. What's the Income if $39/jacket is charged?
Reduce x slightly (even though you can't sell a fraction of a jacket)
to 2.9
The income dropped slightly with a .1 decrease in x
Increase x slightly to 3.1
The income dropped slightly with a .1 increase in x, as expected,
so the peak income really is at x = 3
and $39 per jacket will maximize the weekly profit
|
|
|
