SOLUTION: What is h if ( x^3 + 2 x^2 - 4x + h) ÷ (x + 1) has a remainder of 15?

There are two ways to do the problem, so take your pick:

What is h if  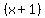has a remainder of 15?

Method 1:

            x² +  x - 5
x + 1)x3 + 2x² - 4x + h
      x3 +  x²
            x² - 4x
            x² +  x
                -5x + h
                -5x - 5
                    h+5

So remainder = h+5  and we are given that the remainder = 15, so

               h+5 = 15
                 h = 10


-----------------------------------------------------  

Method 2:

Memorize this rule known as the "remainder theorem" which says:

When a polynomial is divided by x + r using long* division, the 
remainder obtained is always the same number as is obtained when
-r is substituted for x in the polynomial

*or synthetic, if you've studied that yet.

So since the polynomial 

is divided by x + 1, the remainder obtained is the same number as
is obtained when -1 is substituted for x in the polynomial











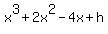
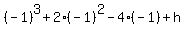
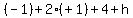
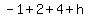
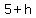So since the remainder obtained is given to be 15,



 

You can do it either way, but your teacher probably wants
you to memorize the remainder theorem, method 2 above.

Edwin