Question 274639: A bridge is built in the shape of a parabolic arch. The bridge has a span of 50 metres and a maximum height of 40 metres. Find the height of the arch 10 metres from the center.
Please & Thank you, i can't even begin to think about how to answer this question.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bridge is built in the shape of a parabolic arch.
The bridge has a span of 50 metres and a maximum height of 40 metres.
Find the height of the arch 10 metres from the center.
:
Here's an idea of what this will look like, where x = the length & y = the height of the bridge

:
We want to find the quadratic equation for this parabola using the form:
ax^2 + bx + c = y; c = 0, so we only have to find a and b
;
We need two x/y coordinates, from the information given.
:
max height is half way: 25 meters and is 40 meters is the height
x = 25, y = 40
25^2a + 25b = 40
625a + 25b = 40
and
the span is given as 50 m and then height = 0
x = 50, y = 0
50^2a + 50b = 0
2500a + 50b = 0
:
we have two equations to find two unknowns, use elimination
:
Multiply the 1st equation by 2, and subtract it from the above equation
2500a + 50b = 0
1250a + 50b = 80
-------------------subtraction eliminates b, find a
1250a = -80
a = 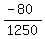
a = -.064
:
Find b using the 1st equation, substitute -.064 for a
-.064(625) + 25b = 40
-40 + 25b = 40
25b = 40 + 40
25b = 80
b = 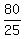
b = 3.2
:
The equation for this parabola: y = -.064x^2 + 3.2x
:
"Find the height of the arch 10 metres from the center."
:
there are two points, 10 meters from the center which is 25 m:
15 meters, substitute 15 for x in our equation, find y (height)
y = -.064(15^2) + 3.2(15)
y = -.064(225) + 3.2(15)
y = -14.4 + 48
y = 33.6 m, 10 meters left of the center
:
How about 10 meter right of center, 35 m?
y = -.064(35^2) + 3.2(35)
y = -.064(1225) + 3.2(35)
y = -78.4 + 112
y = 33.6 m, 10 meters right of the center, same as you would expect in a parabola
:
You can see this agrees with the graph (generated by the equation we just created)
:
Hopefully, this shed some light on this problem for you.
|
|
|