SOLUTION: find the equation whose roots are 5+3i

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: find the equation whose roots are 5+3i      Log On


   

Question 224798: find the equation whose roots are 5+3i
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Find the equation whose roots are 5+3i.

Step 1. We note that i=sqrt%28-1%29 and i%5E2=sqrt%28-1%29%2Asqrt%28-1%29=-1

Step 2. Roots are x=5%2B3i and x=5-3i since complex roots appear in pairs

Step 3. Then we have the following

For x=5+3i, subtract 5+3i from both sides of the equation.

x-%285%2B3i%29=5%2B3i-%285%2B3i%29=0

x-%285%2B3i%29=0 Equation A

for x=5-3i, subtract 5-3ik from both sides of the equation

x-%285-3i%29=5-3i-%285-3i%29=0

x-%285-3i%29=0 Equation B

Step 4. Multiply Equations A and B

%28x-%285%2B3i%29%29%2A%28x-%285-3i%29%29=0

Multiply out the terms using the FOIL method:





%28x-%285%2B3i%29%29%2A%28x-%285-3i%29%29=x%5E2-10x%2B34%29

Step 4. ANSWER: The solution is 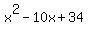x%5E2-10x%2B34%29

Let's check with the quadratic formula given as

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=1, b=-10 and c=34.

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-10x%2B34+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10%29%5E2-4%2A1%2A34=-36.

The discriminant -36 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -36 is + or - sqrt%28+36%29+=+6.

The solution is x%5B12%5D+=+%28--10%2B-+i%2Asqrt%28+-36+%29%29%2F2%5C1+=++%28--10%2B-+i%2A6%29%2F2%5C1+

Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-10%2Ax%2B34+%29



Ignoring the graph below, we have complex roots to this quadratic to be the same ones as given in the problem.

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J