SOLUTION: Struggling on this end. I am supposed to solve by introducing a substitution that transforms equation to quadratic form. (3y)^-2 + (y)^-1 -4=0 Thank you

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Struggling on this end. I am supposed to solve by introducing a substitution that transforms equation to quadratic form. (3y)^-2 + (y)^-1 -4=0 Thank you      Log On


   

Question 224653: Struggling on this end. I am supposed to solve by introducing a substitution that transforms equation to quadratic form.
(3y)^-2 + (y)^-1 -4=0

Thank you
Found 2 solutions by NYC Math Tutor, drj:
Answer by NYC Math Tutor(4) About Me  (Show Source):
You can put this solution on YOUR website!
A quadratic equation is in the form of ax^2 + bx + c
So, what you need to do is change your exponents which are -2, -1, and 0 to 2, 1, and 0. This can be done by multiplying the exponents by -1. So, what you can do is substitute y^-1 for y. Then,
(3y^-1)^-2 + (y^-1)^-1 - 4 = 0
(3^-2)y^2 + y - 4 = 0

Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Solve by introducing a substitution that transforms equation to quadratic form.
%283y%29%5E-2+++%2B+%28y%29%5E-1++-4=0

Step 1. Let x=1%2Fy

Step 2. Substitute x into %283y%29%5E-2+++%2B+%28y%29%5E-1++-4=0

9x%5E2%2Bx-4=0

Step 3. To solve, use the given quadratic formula below

x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where a=9, b=1, and c=-4

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 9x%5E2%2B1x%2B-4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%281%29%5E2-4%2A9%2A-4=145.

Discriminant d=145 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-1%2B-sqrt%28+145+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%281%29%2Bsqrt%28+145+%29%29%2F2%5C9+=+0.613421921044016
x%5B2%5D+=+%28-%281%29-sqrt%28+145+%29%29%2F2%5C9+=+-0.724533032155128

Quadratic expression 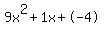9x%5E2%2B1x%2B-4 can be factored:
9x%5E2%2B1x%2B-4+=+9%28x-0.613421921044016%29%2A%28x--0.724533032155128%29
Again, the answer is: 0.613421921044016, -0.724533032155128. Here's your graph:
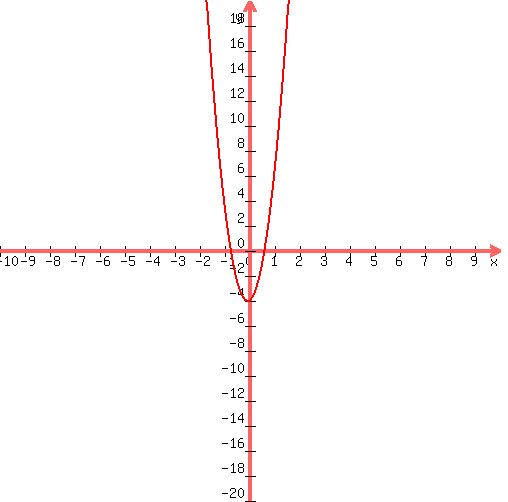graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+9%2Ax%5E2%2B1%2Ax%2B-4+%29



Since x1=0.61342 , then y1=1%2Fx1=1.63

And x2=-0.724533 , then y2=1%2Fx2=-1.38

Step 4. The solution is 1.63 and -1.38

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit
http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit
http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J