Question 1998: Help would be much appreciated with the following question.
The standard equation of a parabola is
y^2=4ax
A general point on this curve has co-ordianates x=at^2, y=2at where t is a (variable) parameter. A point P on the curve has co-ordinates x=a(t1)^2,
y=2a(t1). A chord is drawn through P to meet the parabola again at Q, which has co-ordinates x=a(t2)^2, y=2a(t2).
if this chord passes through the focus S =(a,0) of the parabola finda a simple relationship between (t1) and (t2).
Find the point at which the tangents to the parabola at P and Q meet.
(t1) is my notation for t with a subscript 1
(t2) is my notation for t with a subscript 2.
thankyou in advance!
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! simple relationship between t and u (your t1 and t2..i cannot do subscripts :-( )... PSQ is a straight line, so find its gradient on PS ans SQ...
for PS:
m = 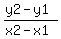
m = 
m = (2t)/(t^2-1)
for SQ:
m = 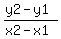
m = 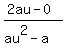
m = (2u)/(u^2-1)
these 2 gradients are the same, so

To find the tangents at P and Q...we need the gradient of the parabola, so differentiate 
2y(dy/dx) = 4a
so dy/dx = 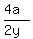
as y=2aT (generic value), then (dy/dx) = 
dy/dx = 1/T
at P, gradient = 1/t, so tangent equation is y=mx+c..sub it
at Q, gradient = 1/u, so tangent equation is y=mx+c..sub it
Got 2 equations then  and and 
equate these for y to find the coordinates of the point where the 2 tangents meet... x=atu, y=a(t+u).
I think this is it..it is late here and i am tired, so please check my answers with your working.
jon
|
|
|