Question 194461: the function h=-5t2+20t+1 models the height, h meters, of a baseball as a function of the time, t seconds, since it was hit. The ball hit the ground before the fielder could catch it. Use the quadratic formula to solve the following problems.
a) How long was the baseball in the air, to the nearest tenth of a second?
b) For how many seconds was the height of the ball at least 16 m?
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! the function h=-5t2+20t+1 models the height, h meters, of a baseball as a function of the time, t seconds, since it was hit. The ball hit the ground before the fielder could catch it. Use the quadratic formula to solve the following problems.
a) How long was the baseball in the air, to the nearest tenth of a second?
.
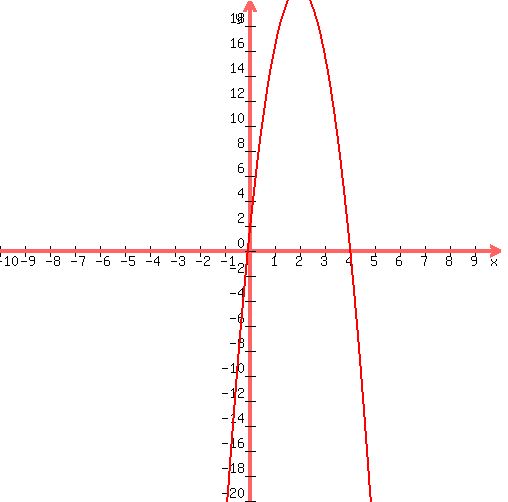
Set h=0 and solve for t
h=-5t2+20t+1
0=-5t2+20t+1
Solving via the quadratic equation yields:
x ={-0.04939, 4.0494}
See below for details...
We can toss out the negative solution leaving:
x = 4.0494 seconds
.
b) For how many seconds was the height of the ball at least 16 m?
Set h=0 and solve for t
h=-5t2+20t+1
16=-5t2+20t+1
0=-5t2+20t-15
0 = (-5t+15)(t-1)
t = {1,3}
This means on the way up at 1 second it reaches 16m and then on the way down at 3 seconds it passes 16m again.
Thus it was in the air for 2 seconds.
.
Quadratic solution for part a:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case  ) has the following solutons:
For these solutions to exist, the discriminant  should not be a negative number.
First, we need to compute the discriminant :  .
Discriminant d=420 is greater than zero. That means that there are two solutions:  .
Quadratic expression  can be factored:
Again, the answer is: -0.0493901531919196, 4.04939015319192.
Here's your graph:
 |
|
|
|
