SOLUTION: Distance from a Point to a Line 13.The equation of a circle with centre O(0,0)is x^2+y^2=10.The points P(1,3) and Q(-3,-1)are endpoints of chord PQ.Find the exact distance from th

The distance from the center to the chord is the
perpendicular distance. So let's draw a line segment
from the center perpendicular to the chord. Label the point
where it intersects the chord R:

 

Drow OP and OQ:



OPQ is isosceles because its two legs 
OP and OQ are radii of the same circle and thus
are equal.

Therefore the altitude OR is the perpendicular 
bisector of PQ.

Therefore R is the midpoint of PQ

We use the midpoint formula

The midpoint between (,) and (,) is given by

(, )

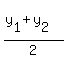So the midpoint R between P(1,3) and Q(-3,-1) is

R(, )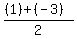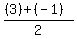

R(, )

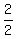R(-1,1)




Now we use the distance formula to find the
distance OR from O(0,0) to R(-1,1)

Distance formula:











Edwin