SOLUTION: jasmine drew a rectangle which is 143sqare mm. ethan drew a rectangle inside of jasmine's which is 35 square mm. ethan's rectangle has a 3 mm border between his and jasmine's recta

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: jasmine drew a rectangle which is 143sqare mm. ethan drew a rectangle inside of jasmine's which is 35 square mm. ethan's rectangle has a 3 mm border between his and jasmine's recta      Log On


   

Question 187616: jasmine drew a rectangle which is 143sqare mm. ethan drew a rectangle inside of jasmine's which is 35 square mm. ethan's rectangle has a 3 mm border between his and jasmine's rectangle. what are the length and width of jasmines rectangle?
after many attempts i believe the answer is 13mm X 11 mm. i have worked backwards but cannot seem to find the equation to use for finding either the length or width. using A = l x w
please help.
donna
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Let x=length of outer rectangle, y=width of outer rectangle


If we draw a picture, we get




Note: the inner rectangle's dimensions are 6 units less than the corresponding on the outer rectangle since there are two 3 unit lengths per side.


Let's set up the equation for the area of the outer rectangle:


A=LW Start with the area of a rectangle formula


143=xy Plug in A=143 (the area of the outer rectangle), L=x, and W=y (the dimensions of the outer rectangle)


143%2Fx=y Divide both sides by "x".


y=143%2Fx Rearrange the equation


---------------------------


Now let's set up the equation for the area of the inner rectangle:


A=LW Go back to the area of a rectangle formula


35=%28x-6%29%28y-6%29 Plug in A=35 (the area of the inner rectangle), L=x-6, and W=y-6 (the dimensions of the inner rectangle)


35=xy-6x-6y%2B36 FOIL


35=x%28143%2Fx%29-6x-6%28143%2Fx%29%2B36 Plug in y=143%2Fx



35=%28143x%29%2Fx-6x-858%2Fx%2B36 Multiply


35=%28143cross%28x%29%29%2Fcross%28x%29-6x-858%2Fx%2B36 Cancel out the common terms.


35=143-6x-858%2Fx%2B36 Simplify


35x=143x-6x%5E2-858%2B36x Multiply EVERY term by the LCD "x" to clear out the fractions.


0=143x-6x%5E2-858%2B36x-35x Subtract 35x from both sides.


0=-6x%5E2%2B144x-858 Combine like terms.


Notice we have a quadratic equation in the form of ax%5E2%2Bbx%2Bc where a=-6, b=144, and c=-858


Let's use the quadratic formula to solve for x


x+=+%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29 Start with the quadratic formula


x+=+%28-%28144%29+%2B-+sqrt%28+%28144%29%5E2-4%28-6%29%28-858%29+%29%29%2F%282%28-6%29%29 Plug in a=-6, b=144, and c=-858


x+=+%28-144+%2B-+sqrt%28+20736-4%28-6%29%28-858%29+%29%29%2F%282%28-6%29%29 Square 144 to get 20736.


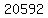
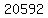x+=+%28-144+%2B-+sqrt%28+20736-20592+%29%29%2F%282%28-6%29%29 Multiply 4%28-6%29%28-858%29 to get 20592


x+=+%28-144+%2B-+sqrt%28+144+%29%29%2F%282%28-6%29%29 Subtract 20592 from 20736 to get 144


x+=+%28-144+%2B-+sqrt%28+144+%29%29%2F%28-12%29 Multiply 2 and -6 to get -12.


x+=+%28-144+%2B-+12%29%2F%28-12%29 Take the square root of 144 to get 12.


x+=+%28-144+%2B+12%29%2F%28-12%29 or x+=+%28-144+-+12%29%2F%28-12%29 Break up the expression.


x+=+%28-132%29%2F%28-12%29 or x+=++%28-156%29%2F%28-12%29 Combine like terms.


x+=+11 or x+=+13 Reduce


So the answers are x+=+11 or x+=+13


This means that the lengths are 11 mm or 13 mm


Since the "length" is usually the longer of the two measurements, let's make the length 13 mm (it doesn't matter either way).


So the width would then be...


y=143%2Fx Go back to the first isolated equation


y=143%2F13 Plug in x=13


y=11 Divide


So the width is 11 mm (note: this is the other answer)


Now subtract 6 mm from each dimension to get


13-6=7 and 11-6=5


So the inner rectangle's dimensions is 7 mm by 5 mm



=============================================================

Answer:


So we just found the following...


Outer Rectangle:

Length = 13 mm, Width = 11 mm


Inner Rectangle:

Length = 7 mm, Width = 5 mm


Check:

143=13*11
143=143...works

35=7*5
35=35...works