Question 182933: Please I need help with: quintun was solving a quadestic equation in the form ax^2+bx+c=0 using the quadestic formula. He made the mistake, however, of switching a and c in the formula and and as a result he got answers that were 3 times the correct answer. Find the product of the roots of the quadratic equation
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please I need help with: quintun was solving a quadestic equation in the form ax^2+bx+c=0 using the quadestic formula. He made the mistake, however, of switching a and c in the formula and and as a result he got answers that were 3 times the correct answer. Find the product of the roots of the quadratic equation.
For any quadratic equation of the form
 ,
the product of the two roots is ,
the product of the two roots is  .
Suppose the two roots are .
Suppose the two roots are  and and  Then
Then  When he switched
When he switched  and and  in the
quadratic formula, he got the roots for in the
quadratic formula, he got the roots for
 ,
to be ,
to be  and and  So their product
So their product  is is 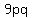 ,
and that had to equal the number ,
and that had to equal the number 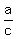 so
so  So we have the system:
So we have the system:
 Clearing of fractions:
Clearing of fractions:
 Solving each for the product
Solving each for the product 
 So we have
So we have
 cross-multiplying gives:
cross-multiplying gives:
 or
or
 so, factoring,
so, factoring,
 So either
So either  or or  Now in the first case, substitution of
of
Now in the first case, substitution of
of 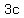 for for  in in
 gives
gives

 ---
In the second case, substitution of
of
---
In the second case, substitution of
of 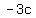 for for  in in
 gives
gives

 So the product of the roots is either
So the product of the roots is either
 or or  Those are the answers!
----------------------------------------
If you want to demonstrate those answers in
specific cases, solve the quadratic equation:
Those are the answers!
----------------------------------------
If you want to demonstrate those answers in
specific cases, solve the quadratic equation:
 and you'll find the solutions
and and you'll find the solutions
and  and and  which have
product which have
product  Then switch
Then switch  and and  and you'll
get the equation and you'll
get the equation
 and you'll find that it has
solutions and you'll find that it has
solutions  and and  which
are 3 times the solutions which
are 3 times the solutions  and and  .
Edwin .
Edwin
|
|
|