Question 178079: Quadratic Relations
39) The vertex of a parabola is (-2,-4). One x-intercept is 7. What is the other x-intercept? (PLEASE)
Thank you very muchhhhhhhhhhhh
Found 2 solutions by gonzo, Mathtut:
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! if the vertex is (-2,-4), then the axis of symmetry would be x = -2.
if one of the x intercepts is 7, this means that the x value is 9 from the axis of symmetry.
this means that the other x intercept would be - 11.
this is because 7 - (-2) = 9
and:
-11 - (-2) = -9
which would make the equation symmetric about the axis of symmmetry.,
---
unfortunately, this leads to complications.
---
if one of the roots of the equation is 7, and the other root of the equation is -11, this means that the equation is (x-7)*(x+11).
this would make the equation equal to x^2 + 4x - 77.
---
since the vertex is at (-2,-4), however, this yields to difficulty.
if x = -2, this equation yields y = 4 -8 - 77 = -81.
this is not consistent with the vertex being at (-2,-4).
it says the vertex is at (-2,-81)
---
i suspect something wrong with the problem setup.
here's why.
---
i can take any equation by multiplying by two roots.
take x = -7 as one of the roots.
take x = 3 as the other root.
my equation will be:
(x+7)*(x-3) = x^2 + 4x - 21.
---
the x coordinate of the vertex of this equation will be -b/2a = -4/2 = -2.
the y coordinate of the vertex of this equation will be f(-2) = 4 - 8 - 21 = -25
the vertex of this equation is therefore (-2,-29).
so far i have:
roots of this equation are:
x = -7
x = 3
and vertex of this equation is:
(-2,-25).
---
if somebody came to me and said:
the vertex of an equation is (-2,-25)
one of the x intercepts is -7
i would have no problem finding the other x intercept and the equation as follows:
i would say the axis of symmetry is x = -2 because the axis of symmetry of an equation that goes up and down is the x coordinate of the vertex.
i would then say that one of the x intercepts is -7.
this means that the distance from the x coordinate to the axis of symmetry is (-2) - (-7) = (-2) + 7 = 5.
to find the other x intercept i would simply add the 5 to the axis of symmetry going in the other direction and i would get (-2) + 5 = (3).
my other x intercept would be 3.
---
i would now have:
x = -7 (given)
vertex = (-2,-25) - again given.
x = 3 (calculated from the information given).
---
since i would now have both roots, i would be able to generate the equation.
(x+7) * (x-3) = x^2 + 4x - 21
---
there would be no conflict between the equation and the vertex of the equation.
---
in the problem that you stated above, there is a conflict which leads me to believe there is something wrong with the information being provided.
---
i'm not a top expert at this and i would not say there is no solution.
i am only saying that i can't find one and that my thinking says there is a problem with the question.
---
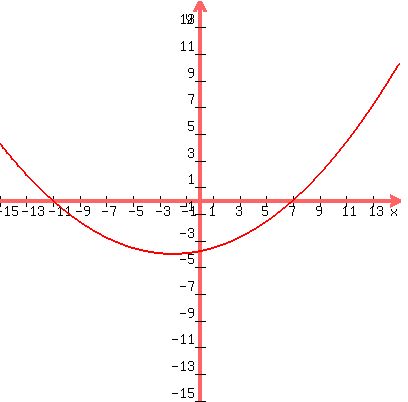
here's a graph of the equation i just showed you would work based on the information i provided for it.

note the x intercepts.
note the vertex.
they are in agreement with the information provided.
---
the next graph shows the information you provided and the equation i was able to calculate from it.
---
you gave the vertex as (-2,-4).
you gave one of the x intercepts at 7
i used that information to calculate the other x intercepts as -11.
i got (x-7)*(x+11) = x^2 + 4x - 77 as the equation based on the x intercepts.
the vertex of this equation is not the same as the vertex you provided.
the vertex i calculated from the equation is (-2,-81).
here's the graph of that equation.

the problem is that the equation generated from the x intercepts does not provide the vertex given, but provides a different vertex, hence the conflict.
---
i suspect a problem with the problem setup.
if you find out different, i would be more than please to know.
i've beaten this to death and come up with the same answer every time.
---
that answer is that there seems to be a problem with the information provided in terms of the vertex and the x intercept. they do not appear to be compatible.
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! We know that the line of symmetry is x=-2 and that one intercept is at (7,0) which is 9 units from the line of symmetry which passes thru (-2,0). if we travel 9 units in the opposite direction then the other x intercept would fall on the point (-11,0)
:
If you use the formula for a parabola to figure out its equation you would use,
:
 where (h,k) is the vertex and a is the vertical stretch where (h,k) is the vertex and a is the vertical stretch
:
we have the vertex and a point on that vertex ..therefore we can find a
:

:
using (7,0) as our known point
:

:

:
a=4/81
:
therefore our equation for this parabola is :
or written with y isolated y=(4/81)(x+2)^2-4}}}
and graphing we see that indeed the x intercepst appear to be where we have them.
:
The reason we cant use just the roots to find the equation of a parabola is as follows:
The parabola (a quadratic) that forms from these roots is the product of these binomials... and a CONSTANT MULTIPLIER which is sometimes called the VERTICAL STRETCH OR COMPRESSION. Many different shapes of parabolas can have the same roots. Heres our case

:
The 'c' doesn't effect the roots... but it does effect the vertical compression or stretch of the parabola.
We cannot write a more specific parabola equation without knowing more information... like vertex, focus, directrix, or another point. We had our extra point and using the parabola formula found our vertical stretch.
:
If we were only given the roots,that is two pieces of information (two points)... but a parabola is a curve. There is no way to extrapolate exact shape based on two points alone (you can only find the equation of a line with two points)
|
|
|