Question 177304: The approximate distance it takes to stop a car, based on the speed the car is travelling, is given in theh following chart:
Miles Per Hour / Stopping Distance (ft)
25 / 62
35 / 106
45 / 161
50 / 195
55 / 228
65 / 306
a- find the quadratic function based on the stopping distance for 55 mph and 65 mph and the fact that at 0 mph the stopping distance is 0 ft.
b- use that equation to predict the stopping distances for 55 mph and 65 mph and compare them with the distances given in the chart.
c- if the equation continues to be valid for higher speeds, how many feet would it take to stop a drag racer that reaches a speed of 230 mph?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The approximate distance it takes to stop a car, based on the speed the car is traveling, is given in the following chart:
Miles Per Hour / Stopping Distance (ft)
25 / 62
35 / 106
45 / 161
50 / 195
55 / 228
65 / 306
:
a- find the quadratic function based on the stopping distance for 55 mph and 65 mph and the fact that at 0 mph the stopping distance is 0 ft.
:
Using the form: ax^2 + bx + c = y,
In this problem c = 0, since y=0 when x=0; Find a and b
:
x=55, y=228
(55^2)a + 55b = 228
3025a + 55b = 228
and
x=65, y=306
(65^2)a + 65b = 306
4225a + 65b = 306
:
use elimination to solve this find a common multiple of 55 & 65
factors 5*11*13 = 715, multiply 1st eq by 13 and the 2nd equation by 11:
:
46475a + 715b = 3366
39325a + 715b = 2964
----------------------subtraction eliminates b, find a
7150a = 402
a = 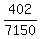
a = .0562
:
find b using eq; 3025a + 55b = 228
.0562(3025) + 5b = 228
170 + 55b = 228
55b = 228 - 170
55b = 58
b = 58/55
b = 1.05
:
Equation: f(x) = .056x^2 + 1.05x
:
:
b- use that equation to predict the stopping distances for 55 mph and 65 mph and compare them with the distances given in the chart.
:
You can calculate this by substitution in the above equation, but I put this
equation into a Ti83, and got:
At 55 mph, 227.755 ft
At 65 mph, 305.695 ft
:
The rest of the values in the table were within 1 mph except 50 mph was 193 ft
:
c- if the equation continues to be valid for higher speeds, how many feet would it take to stop a drag racer that reaches a speed of 230 mph?
:
Again, using the Ti83, I got:
At 230 mph, 3,214.5 ft
:
How about this? did it make sense to you?
|
|
|