SOLUTION: 2x^2-2x+7=0 I have to solve this by completing the square. I solved it but I'm unsure of my answer, I got x= 1/2 + or - i times radical 13 over 2.

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: 2x^2-2x+7=0 I have to solve this by completing the square. I solved it but I'm unsure of my answer, I got x= 1/2 + or - i times radical 13 over 2.       Log On


   

Question 171112: 2x^2-2x+7=0
I have to solve this by completing the square. I solved it but I'm unsure of my answer, I got x= 1/2 + or - i times radical 13 over 2.
Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
You are correct. There are a number of ways to verify your answer, but you can plug in the answer back into the equation and simplify.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Complete the square on 2x%5E2-2x%2B7=0

Step 1, starting from a quadratic in standard form like you have is to put the constant term on the right:

2x%5E2-2x=-7

Step 2, if the coefficient on the x%5E2 term is other than 1, divide by that coefficient.

x%5E2-x=-7%2F2

Step 3, divide the resulting coefficient on the x term by 2 and square the result

%28%28-1%29%2F2%29%5E2=1%2F4

Step 4, add this result to both sides of your equation and collect terms

x%5E2-x%2B1%2F4=-7%2F2%2B1%2F4

x%5E2-x%2B1%2F4=-13%2F4

Step 5, the above result has a perfect square on the left (hence the term "completing the square"), so factor it:

%28x-1%2F2%29%5E2=-13%2F4

Step 6, take the square root of both sides:

x-1%2F2=sqrt%28-13%2F4%29 or x-1%2F2=-sqrt%28-13%2F4%29

Which leads us to a great big oops! because you can't take the square root of a negative number. The solution is to use the imaginary number i which is defined as i%5E2=-1, leaving us with:

x-1%2F2=sqrt%28%28-1%2913%2F4%29 or x-1%2F2=-sqrt%28%28-1%2913%2F4%29
x-1%2F2=sqrt%28-1%29%2Asqrt%2813%2F4%29 or x-1%2F2=-sqrt%28-1%29%2Asqrt%2813%2F4%29
x-1%2F2=i%2Asqrt%2813%2F4%29 or x-1%2F2=-i%2Asqrt%2813%2F4%29

Step 7, isolate x and simplify in each equation

x%5B1%5D=1%2F2%2Bi%2Asqrt%2813%2F4%29=%281%2Bi%2Asqrt%2813%29%29%2F2

x%5B2%5D=1%2F2-i%2Asqrt%2813%2F4%29=%281-i%2Asqrt%2813%29%29%2F2

If you want the exact representation of the roots of the given equation, you are done. If you need a numerical approximation of the imaginary parts of your complex numbers, get out your calculator.

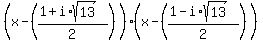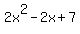Multiplying +%28x-%28%281%2Bi%2Asqrt%2813%29%29%2F2%29%29%28x-%28%281-i%2Asqrt%2813%29%29%2F2%29%29 to verify that the product is, in fact, 2x%5E2-2x%2B7, is left as an exercise for the student. Alternatively, you could just trust me.