Question 170775This question is from textbook
: What type of solution do you get for quadratic equations where D<0?
Give reasons for your answer.
Also provide an example of such a quadratic equation and find the solution of the equation.
I have tried three times and still I am wrong, please help.
This question is from textbook
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! If 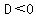 , then the quadratic will have two complex (ie non real) solutions. , then the quadratic will have two complex (ie non real) solutions.
Why? Recall that the quadratic formula is

The discriminant D is everything in the square root. So this means that

Now if 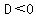 , this means that "D" is negative. Remember you CANNOT take the square root of a negative number. This is why you will NOT get any real solutions if , this means that "D" is negative. Remember you CANNOT take the square root of a negative number. This is why you will NOT get any real solutions if 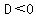
-----------------------------------------------------
For example, let's find the discriminant for 
From 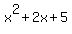 we can see that we can see that  , ,  , and , and 
 Start with the discriminant formula Start with the discriminant formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 
 Multiply Multiply 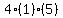 to get to get 
 Subtract Subtract  from from  to get to get 
Since the discriminant is less than zero, this means that there are two complex solutions
--------------------------------------------------------
Now let's use the quadratic formula to find the solutions of 
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 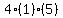 to get to get 
 Subtract Subtract  from from  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Simplify Simplify 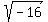 to get to get  . Note: . Note: 
 or or  Break up the expression. Break up the expression.
 or or  Break up the fraction for each case. Break up the fraction for each case.
 or or  Reduce. Reduce.
So our answers are  or or 
Since our answers are complex (ie not real), this verifies our original claim.
|
|
|