Question 126900: A charity collected $2,040 in equal donations from their members to share the cost of a new building. If there were sixty-nine more members, then each member could contribute $23 less. How many members does this charity have?
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let M represent the number of members who donated to the charity. And let C represent the
amount of money each of these members contributed.
.
Given this, then the total amount of money collected can be determined by multiplying
M times C. But the problem tells you that the total amount collected was $2040. Therefore,
we can set these two equal. In equation form this first equation is:
.

.
The problem then tells you that if the number of members is increased by 69 (that would mean
the number of members becomes M + 69) the money collected from each member could be 23 dollars
less (meaning C - 23). The total amount of money collected can then be found by multiplying
the new number of members times the new amount collected from each member and setting
that equal to $2040. In equation form this second equation is:
.

.
We now have two equations involving two unknowns. If a solution exists, this should be
all we need.
.
Returning to the first equation, we can solve for C in terms of M by dividing both sides
of the equation by M to get:
.

.
Then we can substitute the right side of this for C in our second equation as follows:
.

.
You can multiply this out by, one at a time, multiplying each of the terms in the first
set of parentheses times each of the terms in the second set of parentheses and then simplifying
the result by collecting the like terms.
.
Multiplying the M in the first set and each of the two terms in the second set results in:
.

.
Then multiplying the 69 and each of the terms in the second set gives:
.
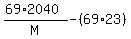
.
Combining these two products on the left side and remembering that they equal 2040 results
in:
.

.
Notice that you have 2040 as a term on each side of the equation. You can eliminate both
by subtracting 2040 from both sides to get:
.

.
Get rid of the denominator M by multiplying both sides of the equation (all terms) by M.
This makes the equation become:
.

.
Just to make things a little more normal, let's first get rid of the minus sign on the term
with the M squared by multiplying the entire equation (both sides and all terms) by -1.
The equation then becomes:
.

.
Rearrange the terms so that they are in descending powers of M:
.

.
Notice now that 23 is a common factor of all the terms on the left side because 69 equals
3 times 23. So get rid of the factor 23 by dividing both sides of the equation (all terms)
by 23 to reduce the equation to:
.

.
Finally, multiply out the term 3*2040 to get 6120 and this makes the equation become:
.

.
This is now in the conventional form of a quadratic equation. You can solve it by using the
quadratic formula or by factoring. (The quadratic formula is a universal way because it
applies to quadratic equations in general. In this case it is probably easier to apply than
trying to factor this quadratic. However, I was able to get the quadratic factored and
in factored form the equation became:}
.

.
This equation will be true if either of the factors is equal to zero because multiplying
the left side by zero will make the left side become equal to the right side. Therefore,
let's set the two factors (one at a time) equal to zero.
.

.
Solve for M by subtracting M from both sides to get:
.

.
That doesn't make sense ... a minus number of members??? Let's toss out that solution and
proceed by setting the second factor equal to zero:
.

.
Solve for M by adding 51 to both sides to get:
.

.
This looks like a good answer. Let's check it.
.
The club currently has 51 members. To get $2040 each member contributed $2040 divided
by 51 and that is $40.
.
If the club had 69 more members (or a total membership of 51 + 69 = 120) and each of these
members contributed $23 less than the $40 originally contributed (or each contributes
$40 - $23 = $17) then you should still have $2040. Multiply 120 members times $17 each
and the product is $2040. Our answer checks.
.
The answer to this problem is that the club currently has 51 members.
.
Sort of complex to explain. I hope this helps you to understand the problem and is clear enough
that you can see one way to solve it.
.
|
|
|