The graph of  is transformed and the new focal point is (16,7).What is the new function?
is transformed and the new focal point is (16,7).What is the new function?
Sorry, but  does not have a focal point. It looks like this
does not have a focal point. It looks like this
 Did you mean
Did you mean  ? It has this graph
? It has this graph
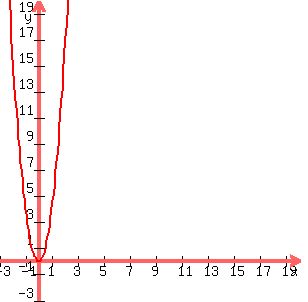 with vertex (0,0) and focal point (0,1)?
If so then the rule is:
To transform the equation of a graph so that
the point (a,b) translates to the new point
(c,d), then replace
x by (x-c+a)
and
y by (y-d+b)
So (a,b) = (0,1) and (c,d) = (16,7)
and we replace
x by (x-c+a) = (x-16+0) = (x-16)
and we replace
y by (y-d+b) = (y-7+1) = (y-6)
replace x by x-16, and y by y-6
with vertex (0,0) and focal point (0,1)?
If so then the rule is:
To transform the equation of a graph so that
the point (a,b) translates to the new point
(c,d), then replace
x by (x-c+a)
and
y by (y-d+b)
So (a,b) = (0,1) and (c,d) = (16,7)
and we replace
x by (x-c+a) = (x-16+0) = (x-16)
and we replace
y by (y-d+b) = (y-7+1) = (y-6)
replace x by x-16, and y by y-6
 Then it has this graph
Then it has this graph
 with focal point (16,7)
Edwin
with focal point (16,7)
Edwin