SOLUTION: Calsho owns a golf course. He presently sells 200 memberships each year for $640 each. He conducts a survey and finds out that for every $40 he raises the price of his membership h

With the current price of $640 per membership, Calsho has 200 customers.

If Calsho raises the price n times by $40 dollars, he will have 200-10n customers,
according to the problem.

So, if the price is p = 640 + 40n dollars, then the number of customers is 200 - 10n.
It is what the problem says.


OK. Now, the revenue is the product of the price by the number of customers.
According our analysis above, we can write this formula for revenue

    R(n) = (640+40n)*(200-10n),

where n is the number of raising the price by 40 dollars.


As you see from formula (1), R(n) is a quadratic function of n

    R(n) = 128000 + 8000n - 6400n - 400n^2 = -400n^2 + 1600n + 128000.    (2)   


We want to find the value of "n" such that the quadratic function (2) has the maximum.
In other words, we want to find the vertex of this parabola.


The vertex is at  n = , where "a" is the coefficient at n^2 and "b" is the coefficient at "n"
in the quadratic form (2).


So,  a= -400, b= 1600, and  =  =  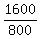= 2.


It means that the optimal price for a membership is  p = 640 + 40*2 = 720;
then the number of customers is  200-10*2 = 180.

So, the predicted revenue will be the product  720*180 = 129600  dollars.


Compare it with the current revenue 640*200 = 128000  dollars and notice the difference.


At this point, I complete my explanations: the problem is just solved.