SOLUTION: The area of a rectangle is 12cm^2. Find the range of possible values of the width of the rectangle if the diagonal is more than 5cm.

This solution assumes the conventional meaning of width, W, to be the shorter side of the rectangle.  The length, L, is taken to be the longer side.



The minimum diagonal of the rectangle will be when L = W = sqrt(12)  (i.e. a square is formed).   However, with these dimensions, the diagonal is only  and that is less than the required 5cm.



Recall the 3-4-5 triangle:

If the length is set to 4cm, the width is then 12/4 = 3cm, and we get 

D = diagonal =  as required.



Hence, 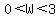 cm   



( The length, L, has bounds  )