Question 1205055: a ball dropped from the top of the tower. A can be modeled by the function h(t)=-9.8t^2+400 and a ball dropped from the top of tower B can be modeled by the function h(t)=-9.8t^2+200, where t is the time in seconds after the ball is dropped and h(t) is its height in meters at that time.
what transformation describes the change from the graph A to graph B?
What does this transformation mean in terms of this situation?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Your teacher or textbook author is mistakenly using -9.8 when it should be -4.9
However, we can imagine this scenario taking place on another planet with a different acceleration of gravity.
Both functions have -9.8t^2 in them.
The key difference is the +400 and +200 at the ends of each.
To go from graph B to graph A, we add 200
B(t) = -9.8t^2 + 200
A(t) = B(t) + 200
A(t) = -9.8t^2 + 200 + 200
A(t) = -9.8t^2 + 400
This moves graph B up 200 units.
In real world context, it means the ball starts 200 meters higher on tower A compared to tower B.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a ball dropped from the top of the tower. A can be modeled by the function h(t)=-9.8t^2+400
and a ball dropped from the top of tower B can be modeled by the function h(t)=-9.8t^2+200,
\where t is the time in seconds after the ball is dropped and h(t) is its height in meters at that time.
what transformation describes the change from the graph A to graph B?
What does this transformation mean in terms of this situation?
~~~~~~~~~~~~~~~~
As it is written, the formulas in your post do not work properly.
Introduction written specially for beginners who don't know the subject AT ALL
The formula in your post is written incorrectly. FATALLY INCORRECTLY, it is what I want to say.
I observed it many times in this forum that the students / (the visitors) write this formula incorrectly.
because they do not understand the meaning of its terms.
So I prepared this text below as a standard introduction to the subject for such students / visitors.
Be calm, you are in good hands, and read my post to the very end.
---------------
If you have the formula for a height given to you as a function of time in the form
h(t) = -at^2 + bt + c, (1)
where "a", "b" and "c" are real numbers, a > 0, then in this formula
(a) the initial height is equal to the coefficient "c" value;
(b) the initial velocity is the coefficient "b" in the formula;
(c) the coefficient "a" value is half of the gravity acceleration.
For the Earth conditions, the gravity acceleration is g = 9.81 m/s^2, or 32 ft/s^2.
THEREFORE, if you use meters for height, you should use the approximate value of g = 10 m/s^2.
So, in this case a =  = 5 (the numerical value).
ALTERNATIVELY, if you use feet for height, you should use the approximate value of g = 32 ft/s^2.
So, in this case a = = 5 (the numerical value).
ALTERNATIVELY, if you use feet for height, you should use the approximate value of g = 32 ft/s^2.
So, in this case a =  = 16 (the numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h = = 16 (the numerical value).
(d) To find the height at the time moment "t", simply substitute the value of "t" into the formula (1) and calculate.
(e) To find the time "t" when the height has a given value h =  , substitute h = , substitute h =  into equation (1)
and solve equation
h(t) = -at^2 + bt + c = into equation (1)
and solve equation
h(t) = -at^2 + bt + c =  . (2)
(f) To find the time when the height is maximal, use the formula . (2)
(f) To find the time when the height is maximal, use the formula
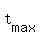 = = 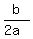 . (3)
(g) To find the maximal height, substitute the time value t= . (3)
(g) To find the maximal height, substitute the time value t= 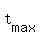 of the formula (3) into the formula (1). of the formula (3) into the formula (1).
That's all you need to know.
After my explanations, you can solve the problem on YOUR OWN now,
but for it, you should have your governing equation written correctly.
---------------
To see numerous examples of solved problems, look into the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
- A flare is launched from a life raft vertically up
in this site.
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
|
|
|