Question 1204485: A soccer ball is kicked off the ground into the air and reaches its maximum height after 2 seconds. After 1 second the height of the ball is 15 feet off the ground. Write a quadratic equation in vertex form to model this situation.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A soccer ball is kicked off the ground into the air and reaches its maximum height after 2 seconds.
After 1 second the height of the ball is 15 feet off the ground.
Write a quadratic equation in vertex form to model this situation.
~~~~~~~~~~~~~~~~~~~~~~~~
They want you find a quadratic equation in vertex form
h(t) = 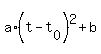 . (1)
It is the general quadratic equation in vertex form.
Now, the problem says that the ball reaches its maximum height after 2 seconds.
It means that the vertex is at t= . (1)
It is the general quadratic equation in vertex form.
Now, the problem says that the ball reaches its maximum height after 2 seconds.
It means that the vertex is at t= 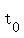 ; in other words, we should take ; in other words, we should take 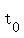 = 2 (seconds).
So, I write
h(t) = = 2 (seconds).
So, I write
h(t) =  . (2)
Next, the problem says that After 1 second the height of the ball is 15 feet off the ground.
It means that I can write the last equation (2) in the form
15 = . (2)
Next, the problem says that After 1 second the height of the ball is 15 feet off the ground.
It means that I can write the last equation (2) in the form
15 = 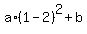 , (3)
substituting 15 ft on the left side and replacing "t" by 1 second in the right side.
It gives me
15 = a + b. (4)
Finally, the problem says that the ball is kicked off the ground.
It means that at t= 0 the height is zero: h = 0.
So, I substitute t= 0 and h= 0 into equation (2), and I get then
0 = , (3)
substituting 15 ft on the left side and replacing "t" by 1 second in the right side.
It gives me
15 = a + b. (4)
Finally, the problem says that the ball is kicked off the ground.
It means that at t= 0 the height is zero: h = 0.
So, I substitute t= 0 and h= 0 into equation (2), and I get then
0 = 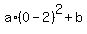 ,
or
0 = 4a + b. (5)
From (5), I have b = -4a and substitute it into equation (4). I get then
15 = a + (-4a) = -3a;
hence
a = ,
or
0 = 4a + b. (5)
From (5), I have b = -4a and substitute it into equation (4). I get then
15 = a + (-4a) = -3a;
hence
a = 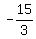 , or a = -5.
Now I am ready to write the final equation from given data
h(t) = , or a = -5.
Now I am ready to write the final equation from given data
h(t) = 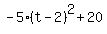 . <<<---=== . <<<---===  +---------------------------------------------+
| But now it is good time to discuss it. |
+---------------------------------------------+
First, having this equation in front of you, you can check that it SATISFIES the problem's conditions.
Second, it is good to re-write this equation in the standard form quadratic equation by opening parentheses
h(t) = -5*t^2 + 10t + 0. (6)
The zero (0) as a constant term is good, because it tells that the initial height is zero at t= 0.
Next, from the standard form (6) everybody, who is familiar with the subject, will say
"HEY, they missed everything in the problem: the leading coefficient a= -5 says that the problem
should consider METERS instead of FEET. For the Earth condition, a= -5 tells that the input numbers
in the condition relate to METERS, not feet".
At this point, I complete my solution and my explanations.
From my post, you learn TWO THINGS:
- first, you learn on HOW TO analyze and solve the problem, step-by-step.
- second, you learn that the problem's formulation, as it is given in the post,
is INCOORRECT and the word "feet" MUST BE replaced by the word "METERS" there.
+---------------------------------------------+
| But now it is good time to discuss it. |
+---------------------------------------------+
First, having this equation in front of you, you can check that it SATISFIES the problem's conditions.
Second, it is good to re-write this equation in the standard form quadratic equation by opening parentheses
h(t) = -5*t^2 + 10t + 0. (6)
The zero (0) as a constant term is good, because it tells that the initial height is zero at t= 0.
Next, from the standard form (6) everybody, who is familiar with the subject, will say
"HEY, they missed everything in the problem: the leading coefficient a= -5 says that the problem
should consider METERS instead of FEET. For the Earth condition, a= -5 tells that the input numbers
in the condition relate to METERS, not feet".
At this point, I complete my solution and my explanations.
From my post, you learn TWO THINGS:
- first, you learn on HOW TO analyze and solve the problem, step-by-step.
- second, you learn that the problem's formulation, as it is given in the post,
is INCOORRECT and the word "feet" MUST BE replaced by the word "METERS" there.
------------------
Solved and COMPLETED.
You should not be surprised by the error in the condition:
at this forum, every second post struggles having ERRORS, fatal or not-fatal.
|
|
|