SOLUTION: Perform partial fraction decomposition for the expression 8+x+6x^2-12x^3/ (3x^2+4)(x^2+7).

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Perform partial fraction decomposition for the expression 8+x+6x^2-12x^3/ (3x^2+4)(x^2+7).      Log On


   

Question 1171058: Perform partial fraction decomposition for the expression 8+x+6x^2-12x^3/ (3x^2+4)(x^2+7).
Found 3 solutions by MathLover1, MathTherapy, greenestamps:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Perform partial fraction decomposition for the expression
%288%2Bx%2B6x%5E2-12x%5E3%29%2F+%28%283x%5E2%2B4%29%28x%5E2%2B7%29%29
%28-12x%5E3%2B6x%5E2%2Bx%2B8%29%2F+%28%283x%5E2%2B4%29%28x%5E2%2B7%29%29
Factor the numerator and denominator:

The form of the partial fraction decomposition is

Write the right-hand side as a single fraction:


The denominators are equal, so we require the equality of the numerators:

Expand the right-hand side:

Collect up the like terms:

The coefficients near the like terms should be equal, so the following system is obtained:
3A%2B3C=-4
3B%2B3D=2
4A%2B21C=1%2F3
4B%2B21D=8%2F3
Solving it (using calculator) we get that A=-5%2F3, B=2%2F3,+C=1%2F3, D=0
Therefore,



...simplfy
Answer:



Answer by MathTherapy(10549) About Me  (Show Source):
You can put this solution on YOUR website!
Perform partial fraction decomposition for the expression 8+x+6x^2-12x^3/ (3x^2+4)(x^2+7).
The other person, as usual has an extremely COMPLEX decomposition. However, it's not her work as she PLAGIARIZED from the following website: 

https://www.emathhelp.net/calculators/algebra-2/partial-fraction-decomposition-calculator/?numer=8%2Bx%2B6x%5E2-12x%5E3&denom=%283x%5E2%2B4%29%28x%5E2%2B7%29&steps=on

Seems like she's trying to IMPRESS some one/people by PLAGIRAIZING other people's work! That's not IMPRESSIVE at all! It's actually DISHONEST!

The more suitable partial decomposition is: !

Answer by greenestamps(13195) About Me  (Show Source):
You can put this solution on YOUR website!


First a comment about the sloppy presentation of the expression....

Here is how the program on this website interprets the expression as you show it:

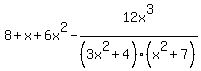
8%2Bx%2B6x%5E2-12x%5E3%2F+%283x%5E2%2B4%29%28x%5E2%2B7%29

That is not the standard interpretation of your expression. By standard rules for order of operations, your expression would be interpreted as

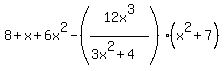
8%2Bx%2B6x%5E2-%2812x%5E3%2F+%283x%5E2%2B4%29%29%2A%28x%5E2%2B7%29

Clearly neither of those expressions is what you meant to show; a partial fraction decomposition does not make sense for either of those expressions.

If you are working on a problem like this, then your knowledge of mathematics is surely advanced enough to know that parentheses are sometimes required to make an expression say what you intended it to say....

The correct form of your expression is (8+x+6x^2-12x^3)/ ((3x^2+4)(x^2+7)):

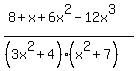
%288%2Bx%2B6x%5E2-12x%5E3%29%2F+%28%283x%5E2%2B4%29%28x%5E2%2B7%29%29

The decomposition will be

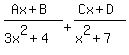
%28Ax%2BB%29%2F%283x%5E2%2B4%29%2B%28Cx%2BD%29%2F%28x%5E2%2B7%29

So we have



Combine the two fractions on the right using a common denominator:



Now the denominators on both sides of the equation are the same, so the numerators must be the same. Expand the numerator on the right and equate coefficients to get systems of equations that you can solve to find A, B, C, and D.




A%2B3C+=+-12
B%2B3D+=+6
7A%2B4C+=+1
7B%2B4D+=+8

Solving those equations gives (A,B,C,D) = (3,0,-5,2), and the decomposition is

3x%2F%283x%5E2%2B4%29%2B%28-5x%2B2%29%2F%28x%5E2%2B7%29