SOLUTION: Hi I need help with a few math problems. I was sick when the teacher gave us the lesson. Im really confused. I will try to explain the problems as best I can. First problem is

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Hi I need help with a few math problems. I was sick when the teacher gave us the lesson. Im really confused. I will try to explain the problems as best I can. First problem is       Log On


   

Question 116762: Hi I need help with a few math problems. I was sick when the teacher gave us the lesson. Im really confused. I will try to explain the problems as best I can.
First problem is Solved By using the Quadratic Formula
1) 4p^2 - 7p = -3
I have no idea what to do in this situation. I know you prefer if I try. But I honestly dont know where to start.
The second Problem is Findind the vertex.
y=x^2 + 2x + 2
Im pretty sure I did this wrong.
I got -1 but im not sure how I got it. The teacher marked it wrong, prolly cause I didnt show all the steps. (shes givin us an opportunity to correct problems)
The third problem is For the parabola
y=x^2 - 6x +8
Find the x intercepts
After doing the work (i prolly did it wrong) I got (x-4)(x-2)=0
and my final answer was x=2, x=4
If you could show the steps to this problem, as well as the others I would really appreciate it. Again any help you guys could give me I would really appreciate it.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
4p%5E2-7p=-3 Start with the given equation


4p%5E2-7p%2B3=0 Move all of the terms to the left side


Let's use the quadratic formula to solve for p:


Starting with the general quadratic

ap%5E2%2Bbp%2Bc=0

the general solution using the quadratic equation is:

p+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29



So lets solve 4%2Ap%5E2-7%2Ap%2B3=0 ( notice a=4, b=-7, and c=3)




p+=+%28--7+%2B-+sqrt%28+%28-7%29%5E2-4%2A4%2A3+%29%29%2F%282%2A4%29 Plug in a=4, b=-7, and c=3



p+=+%287+%2B-+sqrt%28+%28-7%29%5E2-4%2A4%2A3+%29%29%2F%282%2A4%29 Negate -7 to get 7



p+=+%287+%2B-+sqrt%28+49-4%2A4%2A3+%29%29%2F%282%2A4%29 Square -7 to get 49 (note: remember when you square -7, you must square the negative as well. This is because %28-7%29%5E2=-7%2A-7=49.)



p+=+%287+%2B-+sqrt%28+49%2B-48+%29%29%2F%282%2A4%29 Multiply -4%2A3%2A4 to get -48



p+=+%287+%2B-+sqrt%28+1+%29%29%2F%282%2A4%29 Combine like terms in the radicand (everything under the square root)



p+=+%287+%2B-+1%29%2F%282%2A4%29 Simplify the square root (note: If you need help with simplifying the square root, check out this solver)



p+=+%287+%2B-+1%29%2F8 Multiply 2 and 4 to get 8

So now the expression breaks down into two parts

p+=+%287+%2B+1%29%2F8 or p+=+%287+-+1%29%2F8

Lets look at the first part:

x=%287+%2B+1%29%2F8

p=8%2F8 Add the terms in the numerator
p=1 Divide

So one answer is
p=1



Now lets look at the second part:

x=%287+-+1%29%2F8

p=6%2F8 Subtract the terms in the numerator
p=3%2F4 Divide

So another answer is
p=3%2F4

So our solutions are:
p=1 or p=3%2F4

Notice when we graph 4%2Ax%5E2-7%2Ax%2B3 (just replace p with x), we get:

+graph%28+500%2C+500%2C+-2%2C+4%2C+-2%2C+4%2C4%2Ax%5E2%2B-7%2Ax%2B3%29+

and we can see that the roots are p=1 and p=3%2F4. This verifies our answer





#2

To find the vertex, we first need to find the axis of symmetry (ie the x-coordinate of the vertex)
To find the axis of symmetry, use this formula:

x=-b%2F%282a%29

From the equation y=x%5E2%2B2x%2B2 we can see that a=1 and b=2

x=%28-2%29%2F%282%2A1%29 Plug in b=2 and a=1


x=%28-2%29%2F2 Multiply 2 and 1 to get 2



x=-1 Reduce


So the axis of symmetry is x=-1


So the x-coordinate of the vertex is x=-1. Lets plug this into the equation to find the y-coordinate of the vertex.


Lets evaluate 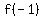f%28-1%29

f%28x%29=x%5E2%2B2x%2B2 Start with the given polynomial


f%28-1%29=%28-1%29%5E2%2B2%28-1%29%2B2 Plug in x=-1


f%28-1%29=%281%29%2B2%28-1%29%2B2 Raise -1 to the second power to get 1


f%28-1%29=%281%29%2B-2%2B2 Multiply 2 by -1 to get -2


f%28-1%29=1 Now combine like terms


So the vertex is (-1,1)


Notice if you graph the equation y=x%5E2%2B2x%2B2 you can see that the vertex is (-1,1). So this visually verifies our answer.





#3


x%5E2-6x%2B8=0 Start with the given equation

%28x-4%29%28x-2%29=0 Factor the left side (note: if you need help with factoring, check out this solver)



Now set each factor equal to zero:
x-4=0 or x-2=0

x=4 or x=2 Now solve for x in each case


So our answer is
x=4 or x=2


Notice if we graph y=x%5E2-6x%2B8 we can see that the roots are x=4 and x=2 . So this visually verifies our answer.


+graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C0%2C+x%5E2-6x%2B8%29+