SOLUTION: my question is Create an example of a quadratic equation that can be factored and solved with non-integer solutions. what would i use? and how would i apply to make this question?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: my question is Create an example of a quadratic equation that can be factored and solved with non-integer solutions. what would i use? and how would i apply to make this question?      Log On


   

Question 1161407: my question is Create an example of a quadratic equation that can be factored and solved with non-integer solutions. what would i use? and how would i apply to make this question?
Found 4 solutions by ikleyn, josgarithmetic, solver91311, KMST:
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.

" . . . how would i apply to make this question? "

What these words mean "apply to make this question ?"



Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
You pick the linear factors that you want. A possible way to get what you want is, the constant term in at least one of them needs to be any non-integer.

%28x-a%29%28x-b%29=0
If a and b are integers, then the solution is the integer a or the integer b.

If a OR b, OR both are not integers, then the solution is NOT integer.

You can pick for a, or b, or both, irrational numbers, or any RATIONAL number not equal to an integer.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Since you didn't specify a quadratic trinomial, a quadratic binomial in the LHS will do just fine.






Or you could try something like:




which factors to:





John

My calculator said it, I believe it, that settles it

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A quadratic equation that can be factored will end up factored into the from K%28x-a%29%28x-b%29=0 , where a and b are the solutions, and K is the coefficient of the term with x%5E2 , with an integer nonzero value for K
In practice, factoring works best when K=1 while a and b are integers.
However, you can factor quadratic equations that have rational solutions that are not integers.
It would be easy to make one.
Let us make a=1%2F2 and b=2%2F3 .
%28x-a%29%28x-b%29=%28x-1%2F2%29%28x-1%2F3%29=x%5E2-%285%2F6%29x%2B1%2F6
x%5E2-5%2F6%2B1%2F6=0 has non-integer solutions,
but students may not find it too easy to factor.
We like integer coefficients, anyway,
so we multiply both sides of the equal sign times 6 to get
6x%5E2-5x%2B1=0 .
You can take any two rational numbers and do the same trick.
That is probably what is expected for the quadratic equation "creation."
You could also start from any product of binomials with integer coefficients where the coefficients of x are not 1.
%282x%2B7%29%283x-1%29=0 is equivalent to 6x%5E2%2B19x-7=0 and would work.
You can see that the solutions are x=-7%2F2 and x=1%2F3 .

There is also the case that if the two solutions are opposites, a and -a, the equation is %28x%2Ba%29%28x-a%29=0 or x%5E2+-a%5E2=0 .
Fr a=1%2F3 we would get x%5E2-1%2F9=0 ,
and present it as the equivalent form
9x%5E2-1=0 , which can be factored as can be factored as

To be a smartalec, I could argue that I can factor x%5E2+-pi=0 into
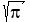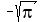%28x-sqrt%28pi%29%29%28x%2Bsqrt%28pi%29%29=0 , to find the non-integer solutions
sqrt%28pi%29 and -sqrt%28pi%29 , but only if the teacher had a sense of humor.