SOLUTION: A projectile is thrown upward so that the its distance above the ground after t seconds is h(t)=-16t^2+308t After how many seconds does it reach its maximum height? What is tha

1.  You may often meet these problems on a projectile thrown vertically upward.

    The equation for the height over the ground usually has ONE OF TWO POSSIBLE forms:

        a)  h(t) = -16*t^2 + v*t + c

                 In this form, the equation is written for the height h(t) over the ground measured in feet.
                 The value of "16" is the half of the value of the gravity acceleration g = 32 ft/s^2.

                 The sign "-" at the first term means that the gravity acceleration is directed down, 
                 while the "y"-axis of the coordinate system is directed vertically up, in the opposite direction.

                 The value of "v" in this equation is the value of the initial vertical velocity. 

                 The value of "c" is the initial height over the ground.

                 The ground level is assumed to be 0 (zero, ZERO). In other words, the origin of the coordinate system is at the ground.


        b)  h(t) = -5*t^2 + v*t + c

                 It is another form of the "height" equation for the same process.

                 In this form, the height h(t) is measured in meters (instead of feet).

                 The value of "5" at the first term is the same gravity acceleration, but this time expressed in "m/s^2" units" g = 10 m/s^2.

                       Actually, more precise value is g = 9.8 m/s^2, therefore, sometimes, this equation goes with the first term -4.9.

                 The value of "v" is the vertical velocity, expressed in m/s.

                 The value of "c" is the initial height over the ground in meters.



2.  In any case, when such problems come from Algebra (as Algebra problems), they are treated in THIS WAY:

    The question "find the maximal height" is the same as "find the maximum of the quadratic form h(t) = -16t^2 + vt + c.

    It doesn't matter that the quadratic function presented as the function of "t" instead of more usual "x" variable.


    Next, when the question is about the maximum/minimum of a quadratic form 

    q(x) = ax^2 + bx + c,

    the Algebra teaches us that the maximum is achieved at   x = .

    
    In your case this value of "t", which provides the maximum height, is  t = 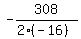 = 9.625 seconds.     


3.  Same problems may come from CALCULUS.  In Calculus, they are treated in this way:

    to find the maximum (minimum), take the derivative and equate it to zero. 

    It will give the equation to find "t".


4.  Same problems may come from PHYSICS.  In Physics, they are treated in this way:

    the maximum height is achieved when the verical velocity becomes equal to zero. 

    It will give the equation to find "t":   t = .


5.  The amazing fact is that different approaches from different branches of Math and Science give the same answer.

    AMAZING ? - Yes, of cource, without doubts for young students.

    AMAZING ? - Yes, but not so much for more mature students, who understand that all these branches of knowledge 

                study the same Nature's phenomenos.  So, the results should (and must) be identical.