Question 1132428: A concert promoter has found that if she sells tickets for $50 each, she can sell 1200 tickets, but for each $5 she raises the price, 50 less people attend. What price should she sell the tickets at to maximize her revenue?
what is the answer to this problem and please explain as to why that is the function used and arrived to that specific answer
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A concert promoter has found that if she sells tickets for $50 each, she can sell 1200 tickets, but for each $5 she raises the price, 50 less people attend.
What price should she sell the tickets at to maximize her revenue?
:
let x = no. of $5 increases and no. of 50 people decreases
then revenue is:
R(x) = (1200-50x)(50+5x)
FOIL and form a quadratic equation
R(x) = 60000 + 6000x - 2500x - 250x^2
R(x) = -250x^2 + 3500x + 60000
simplify, divide by -250, find the axis of symmetry: x = -b/(2*a)
x^2 - 14x - 240 = 0
x = 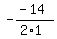
x = 
x = 7 ea $5 increases, $35 + $50 = $85 ticket price gives max revenue
:
Find the amt of the max revenue, find the no. of people
7 * 50 = 350: 1200 - 350 = 850 people
$85 * 850 = $72,250 is the max revenue
;
:
Did this make sense to you??
|
|
|