Question 1122990: if x2 -2x +1 has x-z as a factor, find k
Answer by ikleyn(52750)   (Show Source):
You can put this solution on YOUR website! .
No "k" in the equation (!).
The post is nonsense.
----------------
Comment from student : if x2 -2x +k has x-z as a factor, find k im sorry, i made a typing error
----------------
My response : Apply the Remainder theorem.
It says that the remainder of a polynomial (of ANY polynomial, including yours), when it is divided by a binomial x-z,
is equal to the value of the polynomial at x= z:
The remainder of a polynomial f(x), when it is divided by a binomial x-z,
is equal to f(z).
So, in your case the remainder is equal to zero, since (x-z) is the factor.
It means that 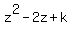 = 0,
which implies k =  .
Solved.
------------------
See the lessons
- Divisibility of polynomial f(x) by binomial x-a and the Remainder theorem
- Solved problems on the Remainder thoerem
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Divisibility of polynomial f(x) by binomial (x-a). The Remainder theorem".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
