.
For example, and as the simplest example, this function q(x) = (x-9)*(x-(-5)),
which is equal to
q(x) = (x-9)*(x+5) =  =
=  .
In more general situation, if you are asked to write the most general form of a quadratic function having the roots
.
In more general situation, if you are asked to write the most general form of a quadratic function having the roots  and
and  ,
then such a function is
q(x) =
,
then such a function is
q(x) = 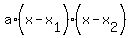 ,
where "a" is the leading coefficient, which can be any non-zero real number.
If you open parentheses and make all necessary multiplications and combine like terms, you will get
q(x) =
,
where "a" is the leading coefficient, which can be any non-zero real number.
If you open parentheses and make all necessary multiplications and combine like terms, you will get
q(x) = 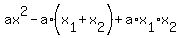 .
.
Explained and solved.