SOLUTION: Matt and Mark have a square tree house with side lengths of x meters, they are currently trying to increase the dimensions of the tree house by 5 meters on both sides. As a result

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Matt and Mark have a square tree house with side lengths of x meters, they are currently trying to increase the dimensions of the tree house by 5 meters on both sides. As a result       Log On


   

Question 1114956: Matt and Mark have a square tree house with side lengths of x meters, they are currently trying to increase the dimensions of the tree house by 5 meters on both sides. As a result the area of the new square tree house is 4 times the area of the original tree house. What is the area of the new tree house?
Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
The condition says


(x+5)^2 = 4x^2


where x is the original dimension of the house.


x^2 + 10x + 25 = 4x^2  ====>

3x^2 - 10x - 25 = 0

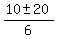x = %2810+%2B-+sqrt%2810%5E2+-+4%2A3%2A%28-25%29%29%29%2F%282%2A3%29 = %2810+%2B-+20%29%2F6.


We are looking for the positive root, which is x = 5.


Answer.  The original size of the square house was 5 meters.  The extended size is 10 meters.

Solved.