.
q is a degree 5 polynomial that passes through the origin, has zeros i and 7−i, and q(3)=1530. Find the equation for q.
~~~~~~~~~~~~~~~~~~~
First of all, your formulation is INCORRECT.
The correct formulation is THIS:
q is a degree 5 polynomial with real coefficients that passes through the origin, has zeros i and 7−i, and q(3)=1530.
Find the equation for q.
Solution
The polynomial q(x) has x as a factor (because it "passes through the origin").
It also has the pairs of the roots i and "-i", as well as (7-i) and (7+i).
Hence, the polynomial has the form
q(x) = ax*(X-i)*(x+i)*(x-(7-i))*(x-(7+i)) =
= ax*(x^2+1)*((x-7)^2 +1).
where "a" is a real coefficient.
Find "a" from the condition
q(3) = 1530 = a*3*(3^2+1)*((-4)^2+1), which is the same as
1530 = 3a*10*17, which implies a =  = 3
Answer. q(x) =
= 3
Answer. q(x) = 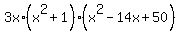 .
.
Solved.