Question 110446: I am trying to graph a quadratic equation....everything was going fine until I tried to get the points for the left side of the graph....they're all over the place...some go below the vertex and it definatly doesnt look like a parabola. Can someone please explain to me how to get the -points? I tried plugging x into the equation but its not working at all...neither are the x and y intercepts, which I have as y=-4 and x=4 and -1, I'm getting so frustrated. The equation is X²+3x-4
I appreciate anyones help!
Bonnie C.
Found 2 solutions by checkley71, solver91311:
Answer by checkley71(8403)   (Show Source): (Show Source):
You can put this solution on YOUR website! y=x^2+3x-4
 (graph 300x200 pixels, x from -6 to 5, y from -10 to 10, y = x^2 +3x -4). (graph 300x200 pixels, x from -6 to 5, y from -10 to 10, y = x^2 +3x -4).
some of the points are (0,-4) obtained by setting x=0 & solving for y
setting y=0 & solving for x we get
x^2+3x-4=0
(x+4)(x-1)=0
x+4
x=-4 answer. (-4,0)
x-1=0
x=1 answer. (1,0)
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's start with what the graph SHOULD look like and go from there.
:

:
Next, let's find the roots of the equation 
:
Looking at the value of the b and c coefficients, the first thing we can tell is that our two factors are going to be of the form 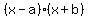 . That's because the sign on the constant term is negative. The sign on the first degree term (3x) being positive tells us that the absolute value of b has to be larger than the absolute value of a in . That's because the sign on the constant term is negative. The sign on the first degree term (3x) being positive tells us that the absolute value of b has to be larger than the absolute value of a in 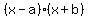 . So what are the possible values for a and b? . So what are the possible values for a and b?
:
+/- 1, +/-2, and +/-4
:
Looking at that, -1 and +4 have a sum of +3, so that looks like our numbers.
:


:
Which means that  or or  , which is to say , which is to say  or or  . Looking at the intercepts you posted, you can see that your signs are reversed. This may be one source of your difficulties. . Looking at the intercepts you posted, you can see that your signs are reversed. This may be one source of your difficulties.
:
Looking at the graph, your y-intercept seems to be correct, but let's check by determining the value of  when when  . By inspection you should see that . By inspection you should see that  , so that intercept point you had was correct. , so that intercept point you had was correct.
:
You didn't share the value of the coordinates you found for the vertex, but the vertex, (h,k), should have an x-coordinate of  , in this case , in this case  . Substitute in the orginial equation to get the y-coordinate of the vertex. In this case, . Substitute in the orginial equation to get the y-coordinate of the vertex. In this case,
:


 . .
:
Having determined these points, you should then be able to select some candidate x values to determine a few more points. I suggest you use 2, -1, -2, -3, and -5. That should give you enough points, assuming careful arithmetic, to plot so that you can draw a smooth curve.
|
|
|