SOLUTION: A gardener has 100 meters of fencing to enclose two adjacent rectangular gardens (see figure). The gardener wants the enclosed area to be 336 square meters. What dimensions should

The gardener/the fence has 3 times the length L and 2 times the width W (it is the FULL wide, not its half).

So the equations are

3L + 2W = 100,       (1)
L*W = 336.           (2)


From (1), W = 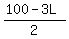. Substitute it into (2) replacing W. You will get

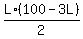 = 336,   or

L*(100-3L) = 672,

100L - 3L^2 = 672,

3L^2 - 100L + 672 = 0.


 =  = .


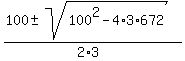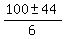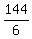 =  = 24   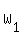      --->   =  = 14.


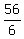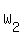 =  =          --->   =  = 36.


Answer.  There are two solutions: 1) the rectangle has the outer dimensions 24 m and 14 m;

                                  2) the rectangle has the outer dimensions  m and 36 m.