Question 1059997: An airplane flies 355 miles to city A . Then, with better winds, it continues on to cityB , 448 miles from A , at a speed 15.8 mi/h greater than on the first leg of the trip. The total flying time was 5.20h . Find the speed at which the plane travelled to city A .
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
An airplane flies 355 miles to city A. Then, with better winds, it continues on to city B, 448 miles from A,
at a speed 15.8 mi/h greater than on the first leg of the trip. The total flying time was 5.20 h .
Find the speed at which the plane traveled to city A.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Your equation is
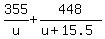 = 5.2.
First addend on the left side is the flying time to get A.
The second addend on the left side is the flying time From A to B.
Solve the equation to get the unknown u, the speed under the question.
As a first step, multiply both sides of the equation by 8*u*(u+15.5).
Then simplify and solve the quadratic equation.
|
|
|
