Question 1059845: The product of two consecutive positive even numbers is 288. By forming and solving an equation, find the larger of the two numbers
Found 3 solutions by acw1213, Alan3354, MathTherapy:
Answer by acw1213(28)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consecutive integers follow one another in an order.
If "2x" is a consecutive integer, it would be 2x, 2x + 1, 2x + 2... etc.
Let's say 2x will represent one of the numbers and 2x + 2 will represent another number.
Multiply them together
2x(2x + 2) = 288
Distribute
4x^2 + 4x = 288
We need to get this equal to zero to be able to solve.
Subtract 288 on both sides.
4x^2 - 4x - 288 = 0
We cannot factor this, so we must use the quadratic formula

In our quadratic equation,
a = 4
b = -4
c = -288
Plug in "a" "b" and "c" and simplify.

Let's simplify the numerator in our square root fraction first.
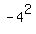 is 16. is 16.
-4(4)(-288) is 4608.
Now we have:

16 + 4608 is 4624

Onto the denominator, 2*4 we know is 8.

We're not done just yet!
We do not know if 4 will be ADDED or SUBTRACTED from the square root of 578 (all over 8), so we have to solve for "x" using BOTH WAYS!
Let's begin with adding.

The square root of 4624 is 68.

4 + 68 is 72.

And finally, 72 divided by 8 is 9.
We have one answer!

Now let's solve with SUBTRACTION

4 - 68 is -64.

-64 divided by 8 is -8.
Our other answer is

Our solutions are x = -8 or x = 9.
We still need to find two possible pairs of numbers,
so plug in -8 for "x" in 2x to find one number, and plug in -8 for "x" in 2x + 2 and find that number.

We have one number, -16.
Now, plug in -8 for "x" in 2x + 2 to find the other number.

We have two numbers in this pair, -16 and -14.
Now, plug in 9 into the same two expressions to get two MORE possible solutions.


We have a total of 4 numbers now.
-16, -14
and
-18, -16.
Find the larger of both sets.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! The product of two consecutive positive even numbers is 288. By forming and solving an equation, find the larger of the two numbers
----------
Find a pair of factors that differ by 2: --> 16 & 18 and -18 & -16
We're done.
===========================
---------
The long way around:
---
x*(x+2) = 288
x^2 + 2x - 288 = 0
Now, find a pair of factors that differ by 2, same as above.
(x-16)*(x+18) = 0
etc.
----------
Extra steps and time for no good reason.
---
The other tutor is trying to get a Master's degree from this problem.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|