Question 1036579: The total cost of 4 apples and 5 oranges is $44. When 1 apple and 2 oranges are removed from the lot,the cost is reduced by $14. Find the cost of 1 apple.
Found 2 solutions by Cromlix, MathTherapy:
Answer by Cromlix(4381)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi there,
The total cost of 4 apples and 5 oranges is $44.
4x + 5y = 44......(1)
hen 1 apple and 2 oranges are removed from the lot,
the cost is reduced by $14.
3x + 3y = 30......(2)
................
4x + 5y = 44......(1)
3x + 3y = 30......(2)
Multiply Eq(1) by 3
Multiply Eq(2) by 4
12x + 15y = 132....(1)
12x + 12y = 120....(2)
Subtract Eq(2) from Eq(1)
.....3y = 12
......y = 4
Substitute y = 4 into Eq(1)
4x + 5y = 44......(1)
4x +5(4) = 44
4x + 20 = 44
4x = 44 - 20
4x = 24
x = 6
Apple costs $6
Orange costs $4
Hope this helps :-)
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The total cost of 4 apples and 5 oranges is $44. When 1 apple and 2 oranges are removed from the lot,the cost is reduced by $14. Find the cost of 1 apple.
Let the price of an apple, and an orange be A, and J, respectively
Then, 4A + 5J = 44 ----- eq (i)
Also, 3A + 3J = 30_____3(A + J) = 3(10)______A + J = 10______J = 10 - A ------ eq (ii)
4A + 5(10 – A) = 44
4A + 50 – 5A = 44
4A – 5A = 44 – 50
- A = - 6
A, or price of 1 apple = 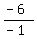 , or , or 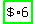
Pretty pricey apple!!
|
|
|