Question 1014084: Word Problem: The sum of two integers is 37 and their product is 342. What are the numbers?
I'm not sure if this is correct but I tried answering it. Here's what I got:
Let: x = be the number
37 - x = be the other number
x(37-x) = 342
37x-x^2 = 342
0 = x^2 - 37x + 342
At this point, I don't know what to do anymore. Please help me.
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! The steps look good, and you used the description to use ONE variable instead of two variables. You would expect the solutions for x in the quadratic equation to be integers.
You can try factoring unless you are not patient enough and you can use formula for general solution of a quadratic equation. Keep going!
Further Note: Try factoring; it should be fairly easy with this.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Word Problem: The sum of two integers is 37 and their product is 342. What are the numbers?
I'm not sure if this is correct but I tried answering it. Here's what I got:
Let: x = be the number
37 - x = be the other number
x(37-x) = 342
37x-x^2 = 342
0 = x^2 - 37x + 342
At this point, I don't know what to do anymore. Please help me.
------------------------------------------------------------
1. Next apply the quadratic formula to solve your quadratic equation.
Do you know what is the quadratic formula?
If not, see these lessons in this site
PROOF of quadratic formula by completing the square
Introduction into Quadratic Equations
2. OR factor your equation
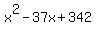 = (x-19)*(x-18)
and obtain immediately the roots x = 19 and x = 18.
Yes, their sum is 18 + 19 = 37, and their product is 18*19 = 342.
3. OR factor the integer 342 as a product of prime numbers: 342 =  and try to get the required numbers.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Word Problem: The sum of two integers is 37 and their product is 342. What are the numbers?
I'm not sure if this is correct but I tried answering it. Here's what I got:
Let: x = be the number
37 - x = be the other number
x(37-x) = 342
37x-x^2 = 342
0 = x^2 - 37x + 342
At this point, I don't know what to do anymore. Please help me.
You can use the quadratic equation to solve, but if you know how to find factors of a trinomial,
you'll see that the 2 factors that multiply to + 342 (ac), and sum to - 37 (b), are: - 19, and - 18
The quadratic now becomes: (x - 19)(x - 18) = 0, and the 
|
|
|
