This Lesson (Fool-Proof Completing the Square, Part I) was created by by prince_abubu(198)   : View Source, ShowAbout prince_abubu:
One of the greatest wonders of quadratic equations is the fact that they have maximum or minimum values. When you graph a quadratic equation, it's a u-shaped curve, either opening up or opening down. Often times, you need to know the coordinate points of the vertex, which is the highest point or lowest point in the quadratic equation's graph, since it has some important real life applications.
A lot of times, a quadratic equation will be thrown at you in the form  . Just by looking at that you can't tell what the coordinates of the vertex are. Completing the square is a series of steps that allow you to rearrange a quadratic equation in standard form to a form where you can pick out the x and y coordinates of the vertex EASILY. . Just by looking at that you can't tell what the coordinates of the vertex are. Completing the square is a series of steps that allow you to rearrange a quadratic equation in standard form to a form where you can pick out the x and y coordinates of the vertex EASILY.
Before we go on, we have to nail down a few things. The first one is actually a "duh!" but we need it BADLY. Say that you have a single number, say 5. If we said 5 + 3 - 3, the answer is still 5. Why would we want to add a number and subtract it back to get to the original number? That's the point
Another thing we need to nail down is the concept of perfect trinomial squares. When we have a binomial, say (x - 3) and we multiply it by itself, so (x - 3)(x - 3) or rewritten as 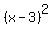 , that turns out to be , that turns out to be 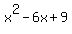 after we perform the FOIL. Notice that the number -3 is doubled to the -6, so you get the second term -6x. Then the -3 gets squared to get the 9, the last term. We're going to think of this whole thing backwards. Say that they throw you a quadratic expression after we perform the FOIL. Notice that the number -3 is doubled to the -6, so you get the second term -6x. Then the -3 gets squared to get the 9, the last term. We're going to think of this whole thing backwards. Say that they throw you a quadratic expression 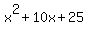 . Are you able to tell that it's a perfect trinomial square? How do you tell!? Take the middle term's coefficient, which is the 10. Divide it by 2. You get 5. Take that 5, square it, you get 25. Does this 25 match the third term of the expression they gave you? It sure does. This means that the original expression they gave you is a perfect trinomial square. If it's a perfect trinomial square, it's guaranteed that it can be written as (x + something) squared. In the case of . Are you able to tell that it's a perfect trinomial square? How do you tell!? Take the middle term's coefficient, which is the 10. Divide it by 2. You get 5. Take that 5, square it, you get 25. Does this 25 match the third term of the expression they gave you? It sure does. This means that the original expression they gave you is a perfect trinomial square. If it's a perfect trinomial square, it's guaranteed that it can be written as (x + something) squared. In the case of 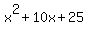 , it can be written as , it can be written as 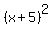 . .
OK. Let's do another example. Let's say 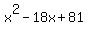 . Is that a perfect trinomial square? Let's see. Let's take the middle coefficient, -18 and cut it in half. That's a -9. Let's square that -9 and we'll get 81. Is 81 the last term of the original expression? Yes. Therefore, . Is that a perfect trinomial square? Let's see. Let's take the middle coefficient, -18 and cut it in half. That's a -9. Let's square that -9 and we'll get 81. Is 81 the last term of the original expression? Yes. Therefore, 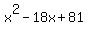 is a perfect trinomial square. Since it's a perfect trinomial square, it's a guarantee that it can be written in the form is a perfect trinomial square. Since it's a perfect trinomial square, it's a guarantee that it can be written in the form  where j is actually the second term's coefficient halved. In this case, we can rewrite the perfect trinomial square where j is actually the second term's coefficient halved. In this case, we can rewrite the perfect trinomial square 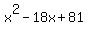 as as 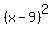 . .
---------------------------------------------------------------------------------------
We're now ready to go through completing the square. Let's work with  . Now that's NOT a perfect trinomial square since 12/2 = 6, and 6 squared is 36, not -7. . Now that's NOT a perfect trinomial square since 12/2 = 6, and 6 squared is 36, not -7.
 <---- We're going to separate the constant term from the rest of the equation with a parentheses. Inside of the parentheses is where part of the action will happen. We need to find a way to get the term inside the parentheses to be a perfect trinomial square. So what we do is to take the 12, divide it by 2, and we get the 6 (Keep this 6 handy). Square the 6 and we get 36. So now, let's add the 36 inside the parentheses. <---- We're going to separate the constant term from the rest of the equation with a parentheses. Inside of the parentheses is where part of the action will happen. We need to find a way to get the term inside the parentheses to be a perfect trinomial square. So what we do is to take the 12, divide it by 2, and we get the 6 (Keep this 6 handy). Square the 6 and we get 36. So now, let's add the 36 inside the parentheses.
 <---- So now we forced the inside of the parentheses to be a perfect trinomial square, however, we messed up the value of the equation when we added the 36. Here's where that old 5 + 3 - 3 trick comes into play. Since we added the 36, we MUST subtract it back out to PRESERVE balance. So actually, the equation should be: <---- So now we forced the inside of the parentheses to be a perfect trinomial square, however, we messed up the value of the equation when we added the 36. Here's where that old 5 + 3 - 3 trick comes into play. Since we added the 36, we MUST subtract it back out to PRESERVE balance. So actually, the equation should be:
 <----- You would subtract the 36 outside the parentheses. <----- You would subtract the 36 outside the parentheses.
 <-------- So we combined the -7 and the -36 because they're like terms. Remember when we said to keep the 6 handy? This is where it comes into play. The second number (12) divided by 2, gives us this 6, which is guaranteed to be the number when the perfect trinomial square is written in the form <-------- So we combined the -7 and the -36 because they're like terms. Remember when we said to keep the 6 handy? This is where it comes into play. The second number (12) divided by 2, gives us this 6, which is guaranteed to be the number when the perfect trinomial square is written in the form  . .
Since We are now done, we're ready to pull out the coordinates of the vertex. The x-coordinate would be 6, and the y-coordinate would be the -43. Notice that you flip the sign of the x-coordinate as you pull it out of the reformed equation, but you don't change the sign of the y-coordinate.
-----------------------------------------------------------------------------------------
Let's do another example: Find the vertex point of  . .
 <----- separate the constant term from everything else. AKA, group the x^2 and the -16x term together inside a set of parentheses. <----- separate the constant term from everything else. AKA, group the x^2 and the -16x term together inside a set of parentheses.
 <---- Take the middle number, the -16. Half it so you'll get the -8. (Keep this -8 handy.) Take that -8 and square it to get the 64. Add the 64 inside the parentheses. This guarantess that the trinomial inside the parentheses is a perfect trinomial square. <---- Take the middle number, the -16. Half it so you'll get the -8. (Keep this -8 handy.) Take that -8 and square it to get the 64. Add the 64 inside the parentheses. This guarantess that the trinomial inside the parentheses is a perfect trinomial square.
 <---- Since we force-added the 64 to make a perfect trinomial square, we must subtract it back out to preserve balance. <---- Since we force-added the 64 to make a perfect trinomial square, we must subtract it back out to preserve balance.
 <---- Combine the two constants outside. Remember that you kept the -8 handy? It's the one used when you write the perfect trinomial square into the form <---- Combine the two constants outside. Remember that you kept the -8 handy? It's the one used when you write the perfect trinomial square into the form  . .
So from looking at the reformed equation, the vertex is at (8,36). Remember to change the sign of the x-coordinate as you pull it out of the new equation. You retain the sign of the y-coordinate as it's copied from the equation.
------------------------------------------------------------------------------------------------
That's not the end of it. What if you have quadratic equations whose a values are not 1? For example, what if we were asked to find the vertex point of  ? Our method above worked because the a value in all of them was 1. In this one equation that was just mentioned, the a-value is 15. What if that a-value were a negative number? What if it were a fraction? Great care must be taken when dealing with a-values that are not 1. Stay tuned for more in Part II. ? Our method above worked because the a value in all of them was 1. In this one equation that was just mentioned, the a-value is 15. What if that a-value were a negative number? What if it were a fraction? Great care must be taken when dealing with a-values that are not 1. Stay tuned for more in Part II.
This lesson has been accessed 22309 times.
|


 : View Source, Show
: View Source, Show