Tutors Answer Your Questions about Quadratic Equations (FREE)
Question 1197633: 15. There are two consecutive even integers. The square of the larger one is three hundred eight more than the smaller one. Which of the following equations could you use to find the smaller integer?
A. (x + 2)^2 - 308 = x
B. (x + 2)^2 + 308 = x
C. (x + 1)^2 + 308 = x
D. (x + 1)^2 = x - 308
E. (x + 1)^2 - 308 = x
F. (x + 2)^2= x - 308
Click here to see answer by greenestamps(13198)   |
Question 1197633: 15. There are two consecutive even integers. The square of the larger one is three hundred eight more than the smaller one. Which of the following equations could you use to find the smaller integer?
A. (x + 2)^2 - 308 = x
B. (x + 2)^2 + 308 = x
C. (x + 1)^2 + 308 = x
D. (x + 1)^2 = x - 308
E. (x + 1)^2 - 308 = x
F. (x + 2)^2= x - 308
Click here to see answer by math_tutor2020(3816)  |
Question 1197633: 15. There are two consecutive even integers. The square of the larger one is three hundred eight more than the smaller one. Which of the following equations could you use to find the smaller integer?
A. (x + 2)^2 - 308 = x
B. (x + 2)^2 + 308 = x
C. (x + 1)^2 + 308 = x
D. (x + 1)^2 = x - 308
E. (x + 1)^2 - 308 = x
F. (x + 2)^2= x - 308
Click here to see answer by josgarithmetic(39617)  |
Question 1197633: 15. There are two consecutive even integers. The square of the larger one is three hundred eight more than the smaller one. Which of the following equations could you use to find the smaller integer?
A. (x + 2)^2 - 308 = x
B. (x + 2)^2 + 308 = x
C. (x + 1)^2 + 308 = x
D. (x + 1)^2 = x - 308
E. (x + 1)^2 - 308 = x
F. (x + 2)^2= x - 308
Click here to see answer by ikleyn(52777)   |
Question 1197659: A skateboarder jumps off a ledge. His path is modeled by the relation
h= -0.8d^2 + 0.8d + 1.6, where h is his height above the ground and d is his horizontal distance from the ledge, both in metres.
a) What is the height of the ledge?
b) Factor to find the zeros of the relation.
c) At what point will the skateboarder land on the ground?
d) Graph the relation.
Click here to see answer by ewatrrr(24785)   |
Question 1197692: The demand function qd=f(p)for a product is quadratic.There points which lie on the demand function are (10,2700),(20,000)and(30,300)
1)determine the equation for the demand function?
2)what quantity will be demanded at a market price of$5?
3)what will be the market price if 1500 units are demanded?
Click here to see answer by ikleyn(52777)   |
Question 1197882: Mr. Reyes wants to enclose the rectangular parking lot beside his house by putting a wire fence on the three sides. If the total length of the wire is 20
meters, find the dimension of the parking lot that will enclose a maximum area
1. if we let w be the width and 1 be the length, what is the expression for the sum of the measures of the three sides of the parking lot?
2. What is the length of the rectangle in terms of the width?
3. Express the area (A) of the parking lot in terms of the width.
4. Fill up the table by having the corresponding areas (A) given w.
5. What have you observed about the area (A) in relation to the width (w)? What happens to area as the measure of the width increases?
6. What is the dependent variable? Independent variable? Explain your answer.
7. From the table of values, plot the points and connect them using a smooth curve?
Click here to see answer by josgarithmetic(39617)  |
Question 1197881: Mr. Reyes wants to enclose the rectangular parking lot beside his house by putting a wire fence on the three sides. If the total length of the wire is 20 meters, find the dimension of the parking lot that will enclose a maximum area
Click here to see answer by ewatrrr(24785)   |
Question 1198105: A soccer ball was kicked upwards. Its path can be modeled by the relation h=-0.2(d-5.5)^2 +7, where h is the ball’s height above the ground and d is the horizontal distance from where the ball was kicked, both in meters.
a) What is the vertex of the parabola?
b) What is the ball’s initial height?
c) Show the graph.
d) What does the vertex represent?
Click here to see answer by ikleyn(52777)   |
Question 1198104: A ball is thrown upward. The path of the ball is modelled by the equation: h=-4.9t^2 + 9.9t + 1, where h is the height of the ball above the ground (in meters) and t is time (in seconds).
Time (s) Height (m)
0.0
0.5
1.0
1.5
2.0
2.5
3.0
a) How long will it take the ball to reach the maximum height?
b) After how many seconds will the ball land?
Click here to see answer by Alan3354(69443)   |
Question 1198226: A cliff driver jumps from the top of a cliff that is 150 feet tall. the distance from the top of the cliff to the water can be modeled by the function y = =- 16x² +150 where x is the time in seconds and y is the height from the ground as the diver jumps. when will the diver be at a height of 15 feet? how long will it take for the diver to splash into the water?
Click here to see answer by math_tutor2020(3816)  |
Question 1198638: 2. Given the equation f(x)=-3(x-4)(x+8), determine the following algebraically.
x-intercepts
y-intercept
Equation of the axis of symmetry
Vertex
3.Convert the following from standard form to vertex form by completing the square.
Click here to see answer by ewatrrr(24785)   |
Question 1198644: 2. Given the equation f(x)=-3(x-4)(x+8), determine the following algebraically. please show your work.
x-intercepts
y-intercept
Equation of the axis of symmetry
Vertex
3.Convert the following from standard form to vertex form by completing the square.
Click here to see answer by MathLover1(20849)   |
Question 1198646: 4.A model rocket is shot straight up from the roof of a school. The height, h, in meters, after t seconds can be approximated by h(t)=-5t2+22t+15. Answer the following questions algebraically, showing all of your work.
What is the height of the school?
When does the rocket hit the ground?
What is the maximum height of the rocket?
How long does it take for the rocket to pass a window that is 10m above the ground? (hint: make h=10, group like terms, then solve the quadratic equation)]
Click here to see answer by math_tutor2020(3816)  |
Question 1198646: 4.A model rocket is shot straight up from the roof of a school. The height, h, in meters, after t seconds can be approximated by h(t)=-5t2+22t+15. Answer the following questions algebraically, showing all of your work.
What is the height of the school?
When does the rocket hit the ground?
What is the maximum height of the rocket?
How long does it take for the rocket to pass a window that is 10m above the ground? (hint: make h=10, group like terms, then solve the quadratic equation)]
Click here to see answer by Alan3354(69443)   |
Question 1198704: Michelle wants her room to be increased in size by at least 40 square meters. She wants to increase the length and the width by the same amount. (a) Find the quadratic function to model this. (b) Determine the initial dimensions (length and width) of the room. (c) Determine by how much do we need to increase the length and width to get Michelle's desired room size.
Click here to see answer by greenestamps(13198)   |
Question 1198747: Answers should be clear, complete, and have proper form.
State the domain and range of the following:
a) f(x)=
b) f(x)=
Application
The parabola f(x)=x2
a) The parabola is
b) The parabola is stretched
3. Describe the transformations
4. Convert the following equation
5. Determine the equation in vertex
Click here to see answer by ikleyn(52777)   |
Question 1198783: 1. State the key features listed for the following parabola: f(x)=-0.5(x+1)2-7
Vertex
Direction of opening
Axis of symmetry
min/max value
range
y-intercept
2. State the domain and range of the following:
a) f(x)=0.5(x+1)2+7
b) f(x)=-3x+4
Click here to see answer by math_tutor2020(3816)  |
Question 1198856: 7. Graph the equation in Desmos or Geogebra. Then answer the following questions. A person throws a ball straight up in the air. The height of a ball, h, in meters, can be modelled by h=-4.9t2+10.78t+1.071, where t is the time in seconds since the ball was thrown.
a)What is the maximum height the ball can reach?
b)How tall is the person that throws the ball up in the air?
c)If the thrower also wants to catch the ball, what time do you think that will occur at?
Click here to see answer by ikleyn(52777)   |
Question 1199009: A ball is thrown upward from 3 meters above ground level with a velocity of 14 meters per second. When does the ball hit the ground?
Here's the explanation:
1. The height starts at 3 meters.
2. It travels at 14 meters pee second or 14(m/s).
In solution step 2 we are told that 14(m/s) = 14t, where t is in seconds.
Where did t come from?
3. Gravity pulls the ball down changing its position by about 5 meters per second squared.
Where did 5 meters per second squared come from?
We are told that it is written like this -5t^2.
Where did the minus 5 come from?
We are further told that -5t^2 is simplified from -(1/2)at^2, where a = 9.8 m/(s^2).
Where did this value of a come from?
The equation created by the given information is h = 3 + 14t - 5t^2.
In my opinion, none of this is given in the given application.
You say?
Click here to see answer by ikleyn(52777)   |
Question 1199157: Show that the real solutions of the equation ax^2 + bx + c = 0 are the reciprocation the real solutions of the equation cx^2 + bx + a = 0. Assume that b^2 - 4ac is greater than or equal to 0.
Can someone get me started here?
Click here to see answer by ikleyn(52777)   |
Question 1199203: How to find the limits of a quadratic function?
lim (x--> 4) g(x)
g(x) = ( 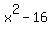 ) )
I thought it would be DNE because I thought 4^+ would be - infinity and 4^- would be + infinity. But the answer is 0 and I don't understand why.
Click here to see answer by ikleyn(52777)   |
Question 1199344: A model rocket is launched from a platform. The trajectory of the
rocket can be modelled by the relation h=−5t^2+100 t+15, where h is the
height of the model rocket in meters and t is the time in seconds.
a) What is the height of the platform?
b) What is the height of the model rocket after 4 seconds?
c) What is the maximum height reached by the rocket? How long does
it take to reach this height?
d) Approximately how long is the rocket in the air?
Click here to see answer by Theo(13342)   |
Question 1199344: A model rocket is launched from a platform. The trajectory of the
rocket can be modelled by the relation h=−5t^2+100 t+15, where h is the
height of the model rocket in meters and t is the time in seconds.
a) What is the height of the platform?
b) What is the height of the model rocket after 4 seconds?
c) What is the maximum height reached by the rocket? How long does
it take to reach this height?
d) Approximately how long is the rocket in the air?
Click here to see answer by ikleyn(52777)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755, 19756..19800, 19801..19845, 19846..19890, 19891..19935, 19936..19980, 19981..20025, 20026..20070, 20071..20115, 20116..20160, 20161..20205, 20206..20250, 20251..20295, 20296..20340, 20341..20385, 20386..20430, 20431..20475, 20476..20520, 20521..20565, 20566..20610, 20611..20655, 20656..20700, 20701..20745, 20746..20790, 20791..20835, 20836..20880, 20881..20925, 20926..20970, 20971..21015, 21016..21060, 21061..21105, 21106..21150, 21151..21195, 21196..21240, 21241..21285, 21286..21330, 21331..21375, 21376..21420, 21421..21465, 21466..21510, 21511..21555, 21556..21600, 21601..21645, 21646..21690, 21691..21735, 21736..21780, 21781..21825, 21826..21870, 21871..21915, 21916..21960, 21961..22005, 22006..22050, 22051..22095, 22096..22140, 22141..22185, 22186..22230, 22231..22275, 22276..22320, 22321..22365, 22366..22410, 22411..22455, 22456..22500, 22501..22545, 22546..22590, 22591..22635, 22636..22680, 22681..22725, 22726..22770, 22771..22815, 22816..22860, 22861..22905, 22906..22950, 22951..22995, 22996..23040, 23041..23085, 23086..23130, 23131..23175, 23176..23220, 23221..23265, 23266..23310, 23311..23355, 23356..23400, 23401..23445, 23446..23490, 23491..23535, 23536..23580, 23581..23625, 23626..23670, 23671..23715, 23716..23760, 23761..23805, 23806..23850, 23851..23895, 23896..23940, 23941..23985, 23986..24030, 24031..24075, 24076..24120, 24121..24165, 24166..24210, 24211..24255, 24256..24300, 24301..24345, 24346..24390, 24391..24435, 24436..24480, 24481..24525, 24526..24570, 24571..24615, 24616..24660, 24661..24705, 24706..24750, 24751..24795, 24796..24840, 24841..24885, 24886..24930, 24931..24975, 24976..25020, 25021..25065, 25066..25110, 25111..25155, 25156..25200, 25201..25245, 25246..25290, 25291..25335, 25336..25380, 25381..25425, 25426..25470, 25471..25515, 25516..25560, 25561..25605, 25606..25650, 25651..25695, 25696..25740, 25741..25785, 25786..25830, 25831..25875, 25876..25920, 25921..25965, 25966..26010, 26011..26055, 26056..26100, 26101..26145, 26146..26190, 26191..26235, 26236..26280, 26281..26325, 26326..26370, 26371..26415, 26416..26460, 26461..26505, 26506..26550, 26551..26595, 26596..26640, 26641..26685, 26686..26730, 26731..26775, 26776..26820, 26821..26865, 26866..26910, 26911..26955, 26956..27000, 27001..27045, 27046..27090, 27091..27135, 27136..27180, 27181..27225, 27226..27270, 27271..27315, 27316..27360, 27361..27405, 27406..27450, 27451..27495, 27496..27540, 27541..27585, 27586..27630, 27631..27675, 27676..27720, 27721..27765, 27766..27810, 27811..27855, 27856..27900, 27901..27945, 27946..27990, 27991..28035, 28036..28080, 28081..28125, 28126..28170, 28171..28215, 28216..28260, 28261..28305, 28306..28350, 28351..28395, 28396..28440, 28441..28485, 28486..28530, 28531..28575, 28576..28620, 28621..28665, 28666..28710, 28711..28755, 28756..28800, 28801..28845, 28846..28890, 28891..28935, 28936..28980, 28981..29025, 29026..29070, 29071..29115, 29116..29160, 29161..29205, 29206..29250, 29251..29295, 29296..29340, 29341..29385, 29386..29430, 29431..29475, 29476..29520, 29521..29565, 29566..29610, 29611..29655, 29656..29700, 29701..29745, 29746..29790, 29791..29835, 29836..29880, 29881..29925, 29926..29970, 29971..30015, 30016..30060, 30061..30105, 30106..30150, 30151..30195, 30196..30240
|

