Question 999860: Given the parabola in which the vertex is the origin and the directrix is a horizontal line passing through the point (0,-7), a student determined that the parabola opens to the right and that the equation of the parabola is y^2=28x. Evaluate the studentís answer. A. The studentís answer is correct. B. The student determined the direction of the parabola correctly but did not correctly determine the equation of the parabola. C. The student determined the equation of the parabola correctly but did not correctly determine the direction of the parabola. D. The student used the equations for a horizontal parabola instead of a vertical parabola. Both the equation and direction of the parabola are incorrect.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's a good reference if you have the time and the inclination to look at it.
http://www.purplemath.com/modules/parabola.htm
the conics form of the equation is:
for vertical orientation:
4p(y-k) = (x-h)^2
for horizontal orientation:
4p(x-h) = (y-k)^2
vertical orientation means the parabola opens up or down.
horizontal orientation means the parabole opens to the left or to the right.
student is given that:
vertex is at the origin (0,0)
directrix is horizontal line through the point (0,-7)
the fact that the directrix is a horizontal line says that the parabole has vertical orientation.
the fact that the directrix is 7 units below the vertex says that the value of p is equal to 7.
that's because p is the distance from the directix to the vertex and also the distance from the focus to the vertex.
since the directrix is 7 units below the vertex, the focus is 7 units above the vertex.
the conics form of the equation is:
4p(y-k) = (x-h)^2
since (h,k) is the vertex and since the vertex is at (0,0), then h = 0 and k = 0.
the equation becomes:
4py = x^2
since p = 7, the equation becomes:
28y = x^2.
the parabola opens up or down (up is the coefficient if the (x-h)^2 term is positive and down if it is negative.
since the coefficient to the (x-h)^2 term is positive, the parabola opens up.
the graph of this parabola is shown below:
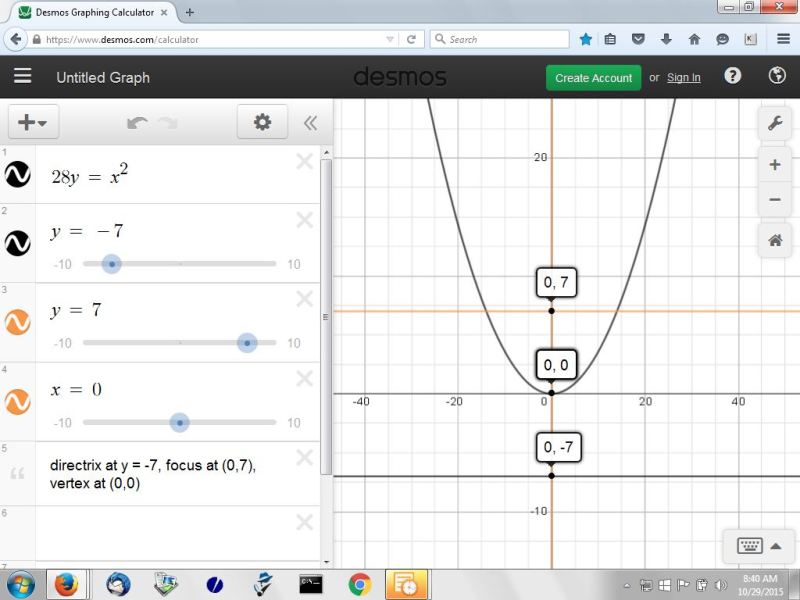
student said orientation was horizontal.
student said equation is 28x = y^2
the student got both the equation and the orientation wrong.
that would be selection D.
|
|
|