Question 99095: Number problems. Find two consecutive positive integers such that the sum of their squares is 85.
Found 2 solutions by Adam, bucky:
Answer by Adam(64)   (Show Source):
You can put this solution on YOUR website! First assumption they are consecutive- they differ by just 1, let's aproximate this and say they are same, then it would  - two nubers and teir sum is 85, but those are actually those squares, so lets take square root 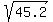 which is around 6.52, whats about 6 and 7 - BINGO :-)
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! Two unknown but consecutive integers can be represented as:
.
x and x+1
.
Their respective squares are x^2 and (x+1)^2, the latter squaring out to be x^2 + 2x + 1
.
So the sum of their squares is:
.
x^2 + x^2 + 2x + 1 and this is equal to 85. Therefore, the equation you need to solve is:
.
2x^2 + 2x + 1 = 85
.
Get rid of the 85 on the right side by subtracting 85 from both sides to get:
.
2x^2 + 2x - 84 = 0
.
Notice that 2 is a common factor of every term in this equation. Therefore, the equation
can be reduced by dividing both sides by 2 to get:
.
x^2 + x - 42 = 0
.
The left side of this equation can be factored to get:
.
(x - 6)(x + 7) = 0
.
This equation will be true if either of the factors equals zero ... because when a factor
is zero, the left side involve a multiplication by zero ... making the entire left side
equal to zero.
.
The two values of x that will make a factor equal to zero can be found by setting
each factor equal to zero to get:
.
x - 6 = 0 which (by adding 6 to both sides) results in x = +6
.
and
.
x + 7 = 0 which (by subtracting 7 from both sides) results in x = - 7
.
But the problem tells you that the answer is to be a positive integer. Therefore,
x = +6 is one of the two consecutive integers and the other must be one more than that
or +7.
.
The two consecutive integers you are looking for are +6 and +7.
.
Check by squaring them both and adding them together to see if their sum is 85
.
6^2 + 7^2 = 36 + 49 = 85
.
It checks so the answer of 6 and 7 is correct. Hope this helps you to understand the problem.
|
|
|
