Question 984228: a ball is thrown into the air at a speed of 115ft/sec from an initial height of 6ft off the ground. How long will it take the ball to hit the ground?
Found 2 solutions by Boreal, KMST:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a parabola with equation y=-16t^2+115t+6
When t=0, the ball is 6 feet off the ground.
Solve for t, and one of the roots should be slightly negative.
y=0 when the ball is on the ground.
quadratic formula
-(1/32)(-115 +/- sqrt (115^2+384) ;;; that is sqrt (13225+384)= sqrt (13993)=116.65
-(1/32) (-115-116.65)=7.24 sec ANSWER
the negative root is -(1/32)(-115+116.65)= -0.05 sec

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a physics problem and a math problem.
If you were given this problem just as a math problem,
along with a formula to use for such a scenario,
you are being taught how to blindly follow instructions without knowing why.
We do that to dogs, but in a reasonable world that should not happen to any person.
On the surface or Earth (or not to far up into space),
gravity pulls objects down towards the ground (and the center of Earth), increasing their downward speed and/or decreasing their upwards speed by 32 ft/sec every second.
That is the acceleration of gravity, usually expressed as
   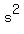 . .
(The value of  varies a little bit from place to place, but 32 ft/sec^2 is a good approximation. varies a little bit from place to place, but 32 ft/sec^2 is a good approximation.
If nothing interferes, the upwards speed/velocity of the ball (in ft/sec) after  seconds is seconds is
 . .
That upwards velocity eventually gets to be zero,
and then goes negative (ball falling) until the ball hits the ground,
when the ground interferes to stop the downwards movement.
In the meantime, the average upwards speed of the ball (in ft/sec) during those  seconds is seconds is
 , ,
the average of the speeds at the beginning and end of those  seconds. seconds.
The upwards distance covered by the ball during those  seconds is seconds is
 . .
The height (in feet) of the ball from the moment it is thrown into the air,  , ,
to a moment  seconds after that is seconds after that is
 , ,
until the ball hits the found and its height in feet is  . .
That  expresses expresses  as a quadratic function of as a quadratic function of  , ,
but it should be defined only for the time between the ball being thrown and the ball hitting the ground,
because we do not know what happened before the ball was thrown into the air, and we do not know what happens to the ball after it hits the ground.
For our function, the domain is   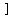 . .
As  is a quadratic function of is a quadratic function of  , ,
it may have up to 2 zeros, and it does.
 <---> <---> has two solutions. has two solutions.
You could solve that equation by using the quadratic formula,
or by completing the square (factoring does not work in this case).
The quadratic formula says that the real solution(s), if any, to an equation of the form
 is/are given by is/are given by  . .
In this case, I was using  instead of {{x}}} , instead of {{x}}} ,
but applying the formula with  , we get , we get
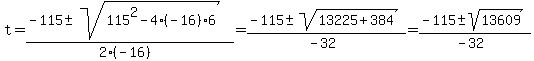 (rounded). (rounded).
The other solution,  ,means nothing to the ball in the problem, ,means nothing to the ball in the problem,
because at a negative time that ball had not been thrown into the air yet.
We could take it to mean the time a ball should have been shot up from the ground to get to a height of 6 feet with a speed of 115 ft/sec at the same time the ball in the problem was thrown into the air.
|
|
|