SOLUTION: what can be the factor in 48x to be equal to 19? this is the equation 6x-19x+8=0. the teaching to us is that we need to multipy the 1st term and 3rd term but it needs to be equal t

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: what can be the factor in 48x to be equal to 19? this is the equation 6x-19x+8=0. the teaching to us is that we need to multipy the 1st term and 3rd term but it needs to be equal t      Log On


   

Question 976246: what can be the factor in 48x to be equal to 19? this is the equation 6x-19x+8=0. the teaching to us is that we need to multipy the 1st term and 3rd term but it needs to be equal to the second term. and im quite confused. can you help me? thank you
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
Are you trying to factor the polynomial, left side member? Do you really have a quadratic trinomial, 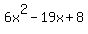6x%5E2-19x%2B8? You have several different combinations of binomials to check.

Something times somethingElse must give product of 6;
Another times SomeOther must give product of 8;
Those are how you can pick coefficients to put into a format.

%28ax%2Bb%29%28cx%2Bd%29=acx%5E2%2Badx%2Bcbx%2Bbd
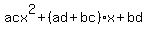
acx%5E2%2B%28ad%2Bbc%29x%2Bbd

You want (ad+bc)=-19, and bd=8, according to corresponding positions for the format of the polynomials. You are likely hoping to find the combination through factorization, so that is what we are testing for. Note also, you need ac=6. You just must try from all the possible combinations until you find the combination that works.

(x-2)(6x-4)
-
(x-4)(6x-2)
-
(x-1)(6x-8)
-
(x-8)(6x-1)
-
.... and there are still other combinations which are possible to check, if any of these listed do not work.




---
I resorted to general solution method for quadratic formula. The solution would be 1%2F2 OR 8%2F3. This would correspond to %28x-1%2F2%29%28x-8%2F3%29=0, certainly not in the form in the way you wanted. This is also not the method you seem expected to use.
---Anyway, that same equation will still have the same solutions if "both side" were multiplied by some constant; such as to clear the denominators of the 2 and the 3. Try first doing the indicated multiplication.

6%28x%5E2-%281%2F2%2B8%2F3%29x%2B4%2F3%29=6%2A0
6x%5E2-6%281%2F2%2B8%2F3%29x%2B6%284%2F3%29=0
6x%5E2-19x%2B8=0

But backtracking just a little to the factored form,
6%28x-1%2F2%29%28x-8%2F3%29=0
Factor the leading coefficient too.
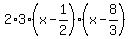
2%2A3%28x-1%2F2%29%28x-8%2F3%29
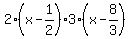
2%28x-1%2F2%29%2A3%28x-8%2F3%29
highlight%28highlight%28%282x-1%29%283x-8%29%29%29

You WOULD have eventually found this too, by making the different possible combinations, as I began with, and testing them. You would have found that THIS would be the combination which worked.