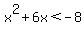
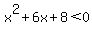
 Critical numbers are -4 and -2
The critical numbers are not part of the solution.
Open circle those on a number line:
----------o-----o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value left of -4, say -5
Substitute x=-5 in
Critical numbers are -4 and -2
The critical numbers are not part of the solution.
Open circle those on a number line:
----------o-----o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value left of -4, say -5
Substitute x=-5 in

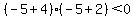
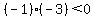
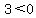 False so we do not shade the interval left of -4
----------o-----o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value between of -4 and =-2, say -3
Substitute x=-3 in
False so we do not shade the interval left of -4
----------o-----o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value between of -4 and =-2, say -3
Substitute x=-3 in

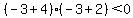
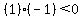
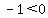 True, so we do shade the interval between -4 and -2
----------o=====o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value right of -4, say 0
Substitute x=0 in
True, so we do shade the interval between -4 and -2
----------o=====o----------------
-7 -6 -5 -4 -3 -2 -1 0 1 2 3
Choose a test value right of -4, say 0
Substitute x=0 in

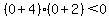
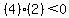
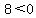 False so we do not shade the interval right of -2
So the set-builder notation is {x|-4 < x < -2}
So the interval notation of the graph is (-4,-2).
Edwin
False so we do not shade the interval right of -2
So the set-builder notation is {x|-4 < x < -2}
So the interval notation of the graph is (-4,-2).
Edwin