Question 9590: A right triangle has one vertex on the graph of y = 3 - x^2, x > 0, and (x, y), another at the origin, and the third on the positive x-axis at (x, 0). Express the area A of the triangle as a function of x.
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! 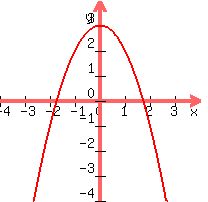
The graph above is for  . One of your vertex lies on the curve. I apologize for the fact that it's quite difficult to draw a triangle that meets what the problem is saying. However, I'll do my best to explain it in words. . One of your vertex lies on the curve. I apologize for the fact that it's quite difficult to draw a triangle that meets what the problem is saying. However, I'll do my best to explain it in words.
You know that the base of the triangle will ALWAYS lie in the x-axis. Its length (the base) is ALWAYS the x, since you're measuring from the origin to wherever x is.
Now the height of your triangle will depend on where your x is, and what the function  will do to it. Actually, the height of your triangle will be the will do to it. Actually, the height of your triangle will be the  . Now, hang on because this is where it'll get tricky. After . Now, hang on because this is where it'll get tricky. After  , ,  will have a negative value. The only thing that happens is that your triangle becomes upside-down, and it'll still have an area. We will force the will have a negative value. The only thing that happens is that your triangle becomes upside-down, and it'll still have an area. We will force the  to be positive by putting it inside absolute value: to be positive by putting it inside absolute value: 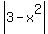 . This way, if . This way, if  , you'll have a positive height for your upside-down triangle. , you'll have a positive height for your upside-down triangle.
So, the area of the triangle is  . The base B is the x. The height is . The base B is the x. The height is  . Since the area depends on x and the function . Since the area depends on x and the function  , the area of the triange becomes a function of x: , the area of the triange becomes a function of x:

|
|
|