Question 9449: Hello-
Thanks in advance for helping me with this problem. I found the answer, but through guess and check, so it would be very helpful if you could tell me how to find the answer mathematicaly.
Mark and David both own a lot of Matchbox cars. Mark owns seven times the square root of the amount David owns. Together they own the square root of 9 multiplyed be the quotient of 27,150 and 181. How many cars do they own in all? How many cars does each boy own? Who owns more?
This really stumped me, but I found an answer.
Mark owns 126 cars.
David owns 324 cars.
Together they own 450 cars.
David owns more.
Thanks again in advance and I can't wait to hear from you.
Sincerely,
Trevor Pierce
Found 2 solutions by rapaljer, mathmaven53:
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = number of cars owned by David
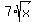 = number Mark owns. = number Mark owns.
Now, the quotient of 29150/181 is just blowing smoke on you. That would be 150, and the square root of 9 (more smoke!!) is 3, so the total cars owned is 150*3 or 450
So, finally, here is the equation:

To solve a radical equation, which this is, you msut isolate the radical term by subtracting x from each side of the equation.

Next, square both sides--that is, square the entire sides:



The numbers here are so large, that you could hardly hope to begin to factor it, although I suspect it DOES factor. You can use the quadratic formula to solve it, or use the pluggable solver by Igor Chudov, the owner of this website.
I'll try the pluggable solver. The graph is not important here, only the solution to the equation.
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=90601 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 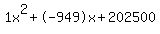 can be factored: can be factored:

Again, the answer is: 625, 324.
Here's your graph:
 |
Notice that the equation DOES factor, and the solutions are 625 and 324. The 625 is more cars than the total, so it must be rejected. That means that David has 324 cars, and Mark has 450 - x = 126 cars.
Good problem. There must be an easier way to solve it. Maybe someone will find it.
R^2 at SCC
Answer by mathmaven53(29)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let m be number of cars owned by Mark
d be number owned by David
m = 7 sqrt d
m + d = (sqrt 9)(27150/181)
The right side is computed to be 450
Then 7 sqrt d + d = 450
(sqrt d)^2 + 7 sqrt d - 450 = 0
by quadratic formula
sqrt d = [-7 + sqrt(49 +4(450))]/2
We use the positve square root in answer else m would be a negative number
Simplifying gives
sqrt d = 18
d = 324
m = 7 sqrt d
= 126
I used a calculator to get these intermediate answers
David has 324 cars and Mark has 126
David has more cars.
|
|
|