SOLUTION: Completing the square 1. X^4+64y^4 2. X^4+y^2+25 3. X^4-11x^2y^2+y^4 Please do help me, My teacher's solution goes like this, and I didn't even understand cuz he's too f

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Completing the square 1. X^4+64y^4 2. X^4+y^2+25 3. X^4-11x^2y^2+y^4 Please do help me, My teacher's solution goes like this, and I didn't even understand cuz he's too f      Log On


   

Question 892918: Completing the square
1. X^4+64y^4
2. X^4+y^2+25
3. X^4-11x^2y^2+y^4

Please do help me,
My teacher's solution goes like this, and I didn't even understand cuz he's too fast.
Ex. x^4+2x^2y^2+9y^4
x^4+9y^4+2x^2y^2
x^4+2x^2(3y^2)+9y^4+2x^2y^2-@x^2(3y^2)
X^4+6x^2y^2+9y^4+2x^2y^2-6x^2y^2
(x^2+3y^2)^2-4x^2y^2
(x^2+3y^2)^2-(2xy)^2
(x^2+3y^2+2xy)(x^2+3y^2-2xy)

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Look for terms that are squares. It is not easy to see them at first. It takes practice.

I will over-explain your teacher's solution:
In 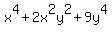x%5E4%2B2x%5E2y%5E2%2B9y%5E4 your teacher sees two squares: %28x%5E2%29%5E2=red%28x%5E4%29 and %283y2%29%5E2=red%289y%5E4%29 .
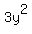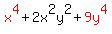The expressions x%5E2 and 3y%5E2 , squared, appear in red%28x%5E4%29%2B2x%5E2y%5E2%2Bred%289y%5E4%29 .
If we add those two expressions and square the sum we have

To make the square 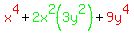red%28x%5E4%29%2Bgreen%282x%5E2%283y%5E2%29%29%2Bred%289y%5E4%29 appear,
your teacher does some plastic surgery to 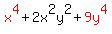red%28x%5E4%29%2B2x%5E2y%5E2%2Bred%289y%5E4%29 .
He takes something out of one end and adds it to another place, just like a plastic surgeon would.
He adds 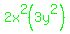green%282x%5E2%283y%5E2%29%29 to "complete the square",
and subtracts the same 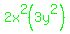green%282x%5E2%283y%5E2%29%29 so as not to really change anything.
Doing that to 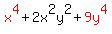red%28x%5E4%29%2B2x%5E2y%5E2%2Bred%289y%5E4%29 , he gets

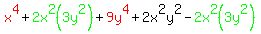
Of course, he knows that green%282x%5E2%283y%5E2%29%29=green%286x%5E2y%5E2%29
and thinks that 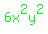green%286x%5E2y%5E2%29 is a more elegant way to write it so he writes

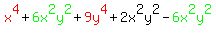
The first three terms are his completed square,

and now he writes that as 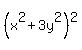%28x%5E2%2B3y%5E2%29%5E2 for short,
and he should have written
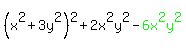
%28x%5E2%2B3y%5E2%29%5E2%2B2x%5E2y%5E2-green%286x%5E2y%5E2%29
Collecting like terms, he gets
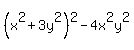
%28x%5E2%2B3y%5E2%29%5E2-4x%5E2y%5E2
Now he realizes that 4x%5E2y%5E2=%282xy%29%5E2 is also a square, and re-writes his expression as
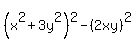
%28x%5E2%2B3y%5E2%29%5E2-%282xy%29%5E2
He likes that because now he has a difference of squares,
and he knows that A%5E2-B%5E2=%28A%2BB%29%28A-B%29 for any two expressions A and B .
So, with A=x%5E2%2B3y%5E2 and B=2xy

Of course, we do not need those parentheses around 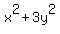x%5E2%2B3y%5E2 and around 2xy ,
I just wrote those parentheses so you would see the separate expressions.
So your teacher writes, without unnecessary parentheses,
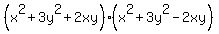
%28x%5E2%2B3y%5E2%2B2xy%29%28x%5E2%2B3y%5E2-2xy%29

1. x%5E4%2B64y%5E4=%28x%5E2%29%5E2%2B%288y%5E2%29%5E2 (I found two squares that are added).
That could be part of the square of a sum:

To make the complete square %28x%5E2%2B16y%5E2%29%5E2=x%5E4%2Bgreen%2816x%5E2y%5E2%29%2B64y%5E4
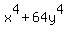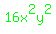
appear in x%5E4%2B64y%5E4 , I add and subtract green%2816x%5E2y%5E2%29
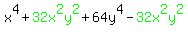to get x%5E4%2Bgreen%2832x%5E2y%5E2%29%2B64y%5E4-green%2832x%5E2y%5E2%29 .
I can re-write that as 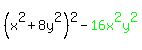%28x%5E2%2B8y%5E2%29%5E2-green%2816x%5E2y%5E2%29 .
Then, since %284xy%29%5E2 is a also a square, I have the difference of squares
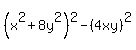%28x%5E2%2B8y%5E2%29%5E2-%284xy%29%5E2%29 , and I can re-write it as
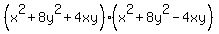
%28x%5E2%2B8y%5E2%2B4xy%29%28x%5E2%2B8y%5E2-4xy%29

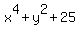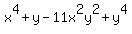For 2. x%5E4%2By%5E2%2B25 and 3. x%5E4%2By-11x%5E2y%5E2%2By%5E4 , I see some squares, but I do not immediately see what to do with them.

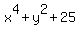2. x%5E4%2By%5E2%2B25 has three squares: x%5E4=%28x%5E2%29%5E2 , y%5E2=%28y%29%5E2 , and 25=5%5E2

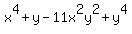3. x%5E4%2By-11x%5E2y%5E2%2By%5E4 has the squares x%5E4=%28x%5E2%29%5E2 andy%5E4=%28y%5E2%29%5E2 .