SOLUTION: Write x^2-6x+7=0 in the form (x-a)^2=b! where a and b are intergers

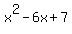
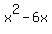
Multiply  by , get 
Square  get .
Add 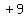 to both sides:



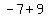Factor the left side, combine terms on right:



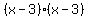
Both factors are the same, so write as one of them squared.
Since 2 = 2!, write 2 that way:



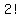That's in the form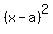 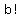, where

a and b are the integers 3 and 2 respetively, and 2 is written as
a factorial 2!.

Edwin