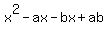
Write -ax-bx as -x(a+b) by factoring out x, then with the x
on the right as -(a+b)x:
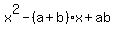
If you have studied that the 2nd term of quadratic with leading
coefficient 1, is the negative of the sum of its roots and that
the last term is the product of the roots, then you know immediately
that the solutions are "a" and "b".
However if you haven't studied that, we can use the quadratic formula.
But it will have to be stated with capital letters "A" and "B" since
the problem itself contains small letters "a" and "b", and we must
avoid using the same letters to refer to different quantities in the
same equation or expression.
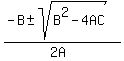with A=1, B=-(a+b) and C=ab
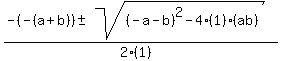
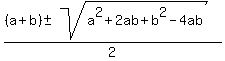
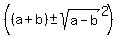
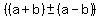Using the +
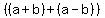
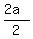
Using the -
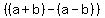
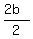
So the long way, the solutions are a and b.
Edwin
