SOLUTION: The width of a rectangle is 8 less than twice its length. If the area of the rectangle is 79 cm^2 what is the length of the diagonal? I am having trouble setting up my initial

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: The width of a rectangle is 8 less than twice its length. If the area of the rectangle is 79 cm^2 what is the length of the diagonal? I am having trouble setting up my initial       Log On


   

Question 881234: The width of a rectangle is 8 less than twice its length. If the area of the rectangle is 79 cm^2 what is the length of the diagonal?
I am having trouble setting up my initial problem. I know that L X W = A and L X H = 79 cm^2.
So if the width is 8 less than twice its length, I set it up as: W = 2L - 8. Then I substituted 2L - 8 into my equation and came up with L(2L-8) = 79
2L^2 - 8L = 79.
Since I can't factor that, I used the quadratic formula to try to solve it. I come up with my length being 8.6. I plugged that into my formula to find the length. I came up with 9.2. I then multiplied 8.6 by 9.2 and came up with 79.12 so I figured I was ok on my area.
I then used a^2 + b^2 = c^2 and came up with 12.59 for my diagonal. The computer tells me I'm wrong. How do I solve this?
Can anyone help me?
Found 3 solutions by KMST, josgarithmetic, MathTherapy:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The width of a rectangle is 8 cm less than twice its length?
Your length was L=8.6 (rounding to the nearest millimeter).
Then your width (in cm) turned out to be W=2L-8=2%2A8.6%2A8=17.2-8=9.2 .
That is a strange result, because it gives you a width that is longer than the length, but I do not see an error in your calculations.
If the sides of a rectangle measure 8.6 cm and 9.2 cm, the diagonal measures about 12.6 cm.
I do not see anything wrong in your calculations.
Maybe there is a typo.
Maybe the problem expects 12.6 for an answer.
Maybe it expects you to write the units.
Maybe it is a question of format, such as "12.6cm" being the answer the computer will accept, but "12.6" or "12.6 cm" being rejected.

Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
X would be another variable. Do NOT use it unless you need this as a variable. Using X for the multiplication operation is not a good way to combine variables.

Let w = width
Let L = length
Your choice of L is better than using the lower-case form, because reading is clearer.

ANALYSIS
w=-8+2L.
wL=79.
Two equations in two unknowns.
wL is area;
wL=79
%28-8%2B2L%29%2AL=79,
and you noticed that you cannot simply divide left and right by 2; but in fact, you CAN. This is not necessary; let's continue.
%282L-8%29L=79
2L%5E2-8L=79
highlight_green%282L%5E2-8L-79=0%29

Maybe that is factorable? I do not care. I will use the general solution of a quadratic equation immediately.
Discriminant: %28-8%29%5E2-4%2A2%2A%28-79%29=696
696=6%2A116=6%2A2%2A58=6%2A2%2A2%2A29=2%2A2%2A2%2A3%2A29

L=%288%2B-+sqrt%282%2A2%2A2%2A3%2A29%29%29%2F%282%2A2%29
Likely you need the positive square root form and value.
L=%288%2B2%2Asqrt%28174%29%29%2F%282%2A2%29
highlight%28L=%284%2Bsqrt%28174%29%29%2F2%29.

Knowing L, now find value of w.
w=2L-8, from transcribed description,
w=2%28%284%2Bsqrt%28174%29%29%2F2%29-8
w=4%2Bsqrt%28174%29-2
highlight%28w=2%2Bsqrt%28174%29%29

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

The width of a rectangle is 8 less than twice its length. If the area of the rectangle is 79 cm^2 what is the length of the diagonal?
I am having trouble setting up my initial problem. I know that L X W = A and L X H = 79 cm^2.
So if the width is 8 less than twice its length, I set it up as: W = 2L - 8. Then I substituted 2L - 8 into my equation and came up with L(2L-8) = 79
2L^2 - 8L = 79.
Since I can't factor that, I used the quadratic formula to try to solve it. I come up with my length being 8.6. I plugged that into my formula to find the length. I came up with 9.2. I then multiplied 8.6 by 9.2 and came up with 79.12 so I figured I was ok on my area.
I then used a^2 + b^2 = c^2 and came up with 12.59 for my diagonal. The computer tells me I'm wrong. How do I solve this?
Can anyone help me?


You did do everything correctly. However, I calculated it, but didn't round until the last number, and I got

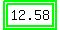highlight_green%28highlight_green%2812.58%29%29 for the length of the diagonal. Maybe that's what it's looking for. Were you asked to round to a 

specific number of decimal places?