Let y² be the whole square
x² + 19x + 92 = y²
x² + 19x + (92 - y²) = 0


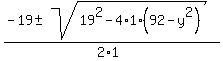








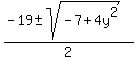 The discriminant -7+4y² must be a perfect square in order that x be
an integer. It also must be an odd square too, so that the numerator
will be even since -19 is odd. But we'll worry about it being odd
later, if necessary. Let the discriminant be z²
discriminant = -7+4y² = z². So,
The discriminant -7+4y² must be a perfect square in order that x be
an integer. It also must be an odd square too, so that the numerator
will be even since -19 is odd. But we'll worry about it being odd
later, if necessary. Let the discriminant be z²
discriminant = -7+4y² = z². So,


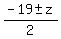 -7+4y² = z²
4y²-z² = 7
(2y-z)(2y+z) = 7
Either both those factor are positive or both are negative
Case 1: If both factors are both positive
Since 7 is prime, the smaller factor
2y-z must be 1 and the larger factor 2y+z = 7
So we have this system of equations:
-7+4y² = z²
4y²-z² = 7
(2y-z)(2y+z) = 7
Either both those factor are positive or both are negative
Case 1: If both factors are both positive
Since 7 is prime, the smaller factor
2y-z must be 1 and the larger factor 2y+z = 7
So we have this system of equations:
 Solve that by substitution or elimination and get
y = 2, z = 3, (z turned out to be odd, so x can be an integer)
Case 2: If they are both negative
Since 7 is prime, the smaller factor
2y+z must be -7 and the larger factor 2y-z = -1
So we have this system of equations:
Solve that by substitution or elimination and get
y = 2, z = 3, (z turned out to be odd, so x can be an integer)
Case 2: If they are both negative
Since 7 is prime, the smaller factor
2y+z must be -7 and the larger factor 2y-z = -1
So we have this system of equations:
 Solve that by substitution or elimination and get
y = -2, z = -3, (z turned out to be odd, so x can be an integer)
Since z = 3 or -3, both values of z are taken care of by:
Solve that by substitution or elimination and get
y = -2, z = -3, (z turned out to be odd, so x can be an integer)
Since z = 3 or -3, both values of z are taken care of by:


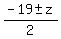


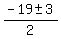 Using the +
Using the +


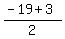



 Using the -
Using the -


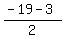

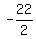

 Two solutions, x = -8, or x = -11
Edwin
Two solutions, x = -8, or x = -11
Edwin