Question 872751: use the given table of values to estimate the volume of the solid formed by revolving
y = f(x),  , about the x-axis, , about the x-axis,
the table :-
_______________________________
x | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
_______________________________
f(x) | 2.3 | 1.4 | 2.9 | 1.1 | 2.4 | 1.6 | 1.9 |
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Plot the 7 points and connect them:
 When we rotate it about the x axis, we'll have a solid figure
with this mid-cross section:
When we rotate it about the x axis, we'll have a solid figure
with this mid-cross section:
 It says just to estimate the volume. So it may be that your teacher
just wants you to average up those 7 y-values like this:
It says just to estimate the volume. So it may be that your teacher
just wants you to average up those 7 y-values like this:
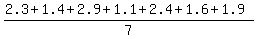 = = 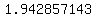 and then assume the volume is about the same volume as a cylinder with
a radius of
and then assume the volume is about the same volume as a cylinder with
a radius of 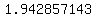 like the cylinder which the green lines
represent a mid-cross section of below: like the cylinder which the green lines
represent a mid-cross section of below:
 If that's the kind of estimate your teacher wants, then we
just use the volume of a cylinder with that average y-value
as a its radius. The cylinder's height h (measured horizontally)
is 3 units,
The formula for the volume of a cylinder is
V =
If that's the kind of estimate your teacher wants, then we
just use the volume of a cylinder with that average y-value
as a its radius. The cylinder's height h (measured horizontally)
is 3 units,
The formula for the volume of a cylinder is
V = 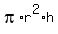 = = 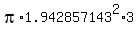 = 35.57565167
So that ought to be a pretty good estimate, about 36 cubic units.
Maybe that's all your teacher wants.
--------------------------------------------
Just for fun, let's find the true volume: and compare:
We'll divide that mid-cross section into 6 little trapezoids: = 35.57565167
So that ought to be a pretty good estimate, about 36 cubic units.
Maybe that's all your teacher wants.
--------------------------------------------
Just for fun, let's find the true volume: and compare:
We'll divide that mid-cross section into 6 little trapezoids:
 Each of those trapezoids is a mid cross section of a frustrum of
a cone, with height h, and the right and left radii are the
values of f(x). The formula for the volume of a frustrum of a
cone is:
Each of those trapezoids is a mid cross section of a frustrum of
a cone, with height h, and the right and left radii are the
values of f(x). The formula for the volume of a frustrum of a
cone is:
  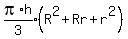 The height of each one is
The height of each one is  so the above will become: so the above will become:
   
  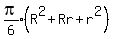  Let the volumes of the frustrums of the cones be V1,...,V6
Total volume =
Let the volumes of the frustrums of the cones be V1,...,V6
Total volume = 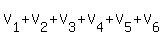
  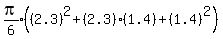  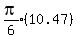
  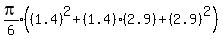  
  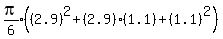  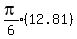
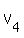    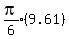
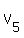  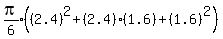  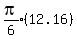
  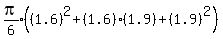  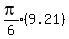 Since all are multiplied by
Since all are multiplied by  Total volume =
Total volume = 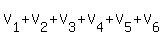 
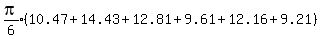  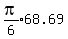 = = 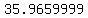 That rounds to 36 cubic units, so the estimate using the cylinder was pretty good.
Edwin
That rounds to 36 cubic units, so the estimate using the cylinder was pretty good.
Edwin
|
|
|